
【题目】某市环保局空气质量监控过程中,每隔x天作为一个统计周期.最近x天统计数据如表
空气污染指数 | [0,50] | (50,100] | (100,150] | (150,200] |
天数 | 15 | 40 | 35 | y |
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)为了创生态城市,该市提出要保证每个统计周期“空气污染指数大于150μg/m3的天数占比不超过15%,平均空气污染指数小于100μg/m3”,请问该统计周期有没有达到预期目标.
【答案】解:(Ⅰ)由图可知,空气污染指数在[0,50]的频率为0.003×50=0.15, 因此样本容量为 ![]() ,
,
空气污染指数在(100,150]的天数为
y=100﹣15﹣50﹣25=10;
画出完整的频率分布直方图,如图所示;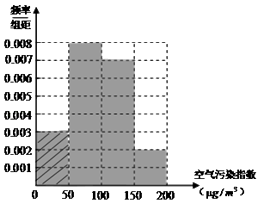
(Ⅱ)在该周期中空气污染指数大于150ug/m3的天数占 ![]() ;
;
该周期的平均空气污染指数为 ![]() ;因此该周期有达到预期目标.
;因此该周期有达到预期目标.
【解析】(Ⅰ)根据频率分布直方图求出对应的频率与样本容量x以及频数y的值, 再补全频率分布直方图;(Ⅱ)计算空气污染指数大于150ug/m3的频率,求数据的平均值,可得结论.
【考点精析】掌握频率分布直方图是解答本题的根本,需要知道频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= ![]() .
.
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A﹣EF﹣C的大小为60°?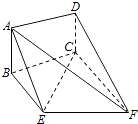
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值;
的极值;
(2)若![]() 时,函数
时,函数![]() 有且只有一个零点,求实数
有且只有一个零点,求实数![]() 的值;
的值;
(3若![]() ,对于区间
,对于区间![]() 上的任意两个不相等的实数
上的任意两个不相等的实数![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣
,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣ ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设直线l:y=kx+1与曲线C交于M、N两点,当线段MN的中点在直线x+2y=0上时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com