
����Ŀ��ij��ѧ��ְ���������߱�����У�ᄊ��¡�ؾ��У�Ϊ�˽�����꼶�С�Ů�����ʦ�ı�����ʱ������������ʦ�������ʦ�ı����ɼ��У��ֱ����ȡ9����ʦ�ijɼ�����λ�����ӣ�������������ľ�Ҷͼ������Ů�������������һ������ģ������ȷ�ϣ�����������־�������ԣ�����ͼ����a��ʾ���涨��������ʱ������19����ʱ���ɼ�Ϊ���㣮
��1�����С�Ů���������ʱ��ƽ��ֵ��ͬ����a��ֵ��
��2����Ů�����ƽ����ʱ����������ƽ����ʱ�ĸ��ʣ�
���𰸡��⣺��1�������⣬�ã�![]() (18+15+16+19+13+21+25+20+23)=
(18+15+16+19+13+21+25+20+23)=![]() (18+16+15+19+19+13+26+21+20+a����
(18+16+15+19+19+13+26+21+20+a����
��� a=3��
��2���衰Ů�����ƽ����ʱ����������ƽ����ʱ��Ϊ�¼�A��
������a=0��1��2����9������10�ֿ��ܣ�
�ɣ�1����֪����a=3ʱ��Ů����ƽ����ʱ��ͬ��
���Ե�a=4ʱŮ�����ƽ����ʱ����������ƽ����ʱ������6�ֿ��ܣ�
����Ů�����ƽ����ʱ����������ƽ����ʱ�ĸ���Ϊ![]() ��
��
����������1�������⣬��![]() (18+15+16+19+13+21+25+20+23)=
(18+15+16+19+13+21+25+20+23)=![]() (18+16+15+19+19+13+26+21+20+a�����ɴ������a��ֵ��
(18+16+15+19+19+13+26+21+20+a�����ɴ������a��ֵ��
��2���衰Ů�����ƽ����ʱ����������ƽ����ʱ��Ϊ�¼�A��������a=0��1��2����9������10�ֿ��ܣ��ɴ������Ů�����ƽ����ʱ����������ƽ����ʱ�ĸ��ʣ�
�����㾫�������ڱ��⿼�����ɢ�������������ֲ��У���Ҫ�˽����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в��ܵó���ȷ�𰸣�


 Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ��a��b��0������ΪF1����
��a��b��0������ΪF1���� ![]() ��0����e=
��0����e= ![]() �� ��������ԲC�ķ��̣�
�� ��������ԲC�ķ��̣�
������ͼ����R��x0 �� y0������ԲC��һ���㣬��ԭ��O��Բ��x��x0��2+��y��y0��2=4���������ߣ��ֱ���Բ�ڵ�P��Q����ֱ��OP��OQ��б�ʴ��ڣ�����Ϊk1 �� k2 �� ��֤��k1k2Ϊ��ֵ��
�����ڣ��������£�����OP2+OQ2�Ƿ�Ϊ��ֵ�����ǣ������ֵ�������ǣ�˵�����ɣ�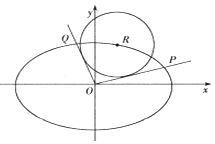
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() .
.
��1����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
��2�������⡰![]() ��
��![]() ��Ϊ�����⣬��ʵ��
��Ϊ�����⣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() �ķ���
�ķ���![]() �Ľ⼯��ǡ����һ��Ԫ�أ���ʵ��
�Ľ⼯��ǡ����һ��Ԫ�أ���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
�� ![]() ��
�� ![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() �е�.
�е�.
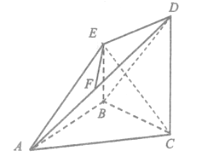
����֤���� ![]() ƽ��
ƽ��![]() ��
��
������ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ���敜���ԭ���������Ƽ�ͬ����������족.���С��ݡ��ǽ���������ơ��Ǽ�����ĸ�.ԭ������˼�ǣ���������ƽ��ƽ�������������壬����һƽ����������ƽ��ƽ���ƽ�����أ������ص�����������������ȣ����������������������.��ͼ��ʾ���ڿռ�ֱ������ϵ![]() ������ƽ��
������ƽ��![]() �ڣ�������
�ڣ�������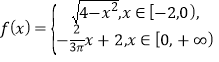 ��ͼ����
��ͼ����![]() ��Χ��һ���������
��Χ��һ���������![]() ��������
��������![]() ��
��![]() �������������4����λ���õ���������ͼһ.����һ����֮�ȸߵ�Բ����ͼ����������������
�������������4����λ���õ���������ͼһ.����һ����֮�ȸߵ�Բ����ͼ����������������![]() �����ȣ����Բ�������Ϊ�� ��
�����ȣ����Բ�������Ϊ�� ��
A. ![]() B.
B. ![]() C. 2
C. 2![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����k��0������f��x��=![]() +x+kln|x��1|��
+x+kln|x��1|��
��1�����ۺ���f��x���ĵ����ԣ�
��2��������f��x����������ֵ�㣬��0���ȣ���ʱ��֤������2k��1��sin��+��1��k��sin[��1��k����]��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ��������
��������![]() .
.
��I����֤��![]() �ǵȱ����У�
�ǵȱ����У�
��II����֤��![]() ���ǵȱ�����.
���ǵȱ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ��������ԭ�㣬������x���ϣ�������Ϊ![]() �� �Ҿ�����M��4��1����ֱ��l��y=x+m����Բ�ڲ�ͬ������A��B��
�� �Ҿ�����M��4��1����ֱ��l��y=x+m����Բ�ڲ�ͬ������A��B��
��������Բ�ķ��̣�
������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��У�Ͳ͵ĸ�һ�꼶ѧ����440�����߶��꼶ѧ����460���������꼶ѧ����500����Ϊ�˽�ѧУʳ�õķ�������������÷ֲ�����ķ������г�ȡ70��ѧ�����г������飬��ѧ����ʳ�õġ���������ȡ��롰�۸�����ȡ�����Ϊ����ȼ���1�����ܲ����⣩��2���������⣩��3����һ�㣩��4�������⣩��5���������⣩����ͳ�ƽ�����±������������Ϊx���۸������Ϊy����
y | �۸������ | |||||
1 | 2 | 3 | 4 | 5 | ||
�� | 1 | 1 | 1 | 2 | 2 | 0 |
2 | 2 | 1 | 3 | 4 | 1 | |
3 | 3 | 7 | 8 | 8 | 4 | |
4 | 1 | 4 | 6 | 4 | 1 | |
5 | 0 | 1 | 2 | 3 | 1 | |
��1����߶��꼶����ȡѧ��������
��2����������ȡ�Ϊ3ʱ��5�����۸�����ȡ����ݵķ��
��3��Ϊ���ʳ�÷����������ִ�x��3��2��y��4������ѧ���������ȡ���������������������һ�˵ġ���������ȡ�Ϊ1�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com