
【题目】在四面体![]() 中,
中,![]() ,则四面体体积最大时,它的外接球半径
,则四面体体积最大时,它的外接球半径![]() _________.
_________.
【答案】![]()
【解析】
由题意画出图形,取AB中点E,连接CE,DE,设AB=2x(0<x<1),则CE=DE=![]() ,可知当平面ABC⊥平面ABD时,四面体体积最大,写出体积公式,利用导数求得体积最大时的x值,再由△ABD的外心G与△ABC的外心H作两个三角形所在平面的垂线,可得交点O为四面体ABCD的外接球的球心,然后求解三角形得答案.
,可知当平面ABC⊥平面ABD时,四面体体积最大,写出体积公式,利用导数求得体积最大时的x值,再由△ABD的外心G与△ABC的外心H作两个三角形所在平面的垂线,可得交点O为四面体ABCD的外接球的球心,然后求解三角形得答案.
如图,

取AB中点E,连接CE,DE,
设AB=2x(0<x<1),则CE=DE=![]() ,
,
∴当平面ABC⊥平面ABD时,四面体体积最大,
为V=![]() =
=![]() =
=![]() .
.
V′=![]() ,当x∈(0,
,当x∈(0,![]() )时,V为增函数,当x∈(
)时,V为增函数,当x∈(![]() ,1)时,V为减函数,
,1)时,V为减函数,
则当x=![]() 时,V有最大值.
时,V有最大值.
设△ABD的外心为G,△ABC的外心为H,
分别过G、H作平面ABD、平面ABC的垂线交于O,则O为四面体ABCD的外接球的球心.
在△ABD中,有sin![]() ,则cos
,则cos![]() ,
,
∴sin![]() =
=![]() .
.
设△ABD的外接圆的半径为r,则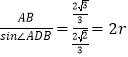 ,即DG=r=
,即DG=r=![]() .
.
又DE=![]() ,∴OG=HE=GE=
,∴OG=HE=GE=![]() .
.
∴它的外接球半径R=OD=![]() .
.
故答案为:![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】1,4,9,16……这些数可以用图1中的点阵表示,古希腊毕达哥拉斯学派将其称为正方形数,记第![]() 个数为
个数为![]() .在图2的杨辉三角中,第
.在图2的杨辉三角中,第![]() 行是
行是![]() 展开式的二项式系数
展开式的二项式系数![]() ,
,![]() ,…,
,…,![]() ,记杨辉三角的前
,记杨辉三角的前![]() 行所有数之和为
行所有数之和为![]() .
.

(1)求![]() 和
和![]() 的通项公式;
的通项公式;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如下四个命题:①在线性回归模型中,相关指数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 的贡献率,
的贡献率,![]() 越接近于
越接近于![]() ,表示回归效果越好;②在回归直线方程
,表示回归效果越好;②在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于
个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于![]() ;④对分类变量
;④对分类变量![]() 与
与![]() ,对它们的随机变量
,对它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,则“
越小,则“![]() 与
与![]() 有关系”的把握程度越大.其中正确命题的序号是__________.
有关系”的把握程度越大.其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 |
|
|
|
甲未参加 |
|
|
|
总计 |
|
|
|
(1)求![]() 的值,据此能否有
的值,据此能否有![]() 的把握认为球队胜利与甲球员参赛有关;
的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:![]() ,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:
,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:![]() .则:
.则:
1)当他参加比赛时,求球队某场比赛输球的概率;
2)当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
3)如果你是教练员,应用概率统计有关知识.该如何使用乙球员?
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一年级300名学生对历史、地理学科的选课情况,对学生进行编号,用1,2,…,300表示,并用![]() 表示第
表示第![]() 名学生的选课情况,其中根据如图所示的程序框图,下列说法错误的是( )
名学生的选课情况,其中根据如图所示的程序框图,下列说法错误的是( )

![]()
![]()
A. ![]() 为选择历史的学生人数;
为选择历史的学生人数;
B. ![]() 为选择地理的学生人数;
为选择地理的学生人数;
C. ![]() 为至少选择历史、地理一门学科的学生人数;
为至少选择历史、地理一门学科的学生人数;
D. ![]() 为选择历史的学生人数与选择地理的学生人数之和
为选择历史的学生人数与选择地理的学生人数之和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 的坐标为
的坐标为![]() 的面积为
的面积为![]() ,过点
,过点![]() 的动直线
的动直线![]() 被椭圆
被椭圆![]() 所截得的线段
所截得的线段![]() 长度的最小值为
长度的最小值为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ) ![]() 是椭圆
是椭圆![]() 上异于顶点的一点,且直线
上异于顶点的一点,且直线![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 的半径为
的半径为![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,求
,求![]() 的最大值,并求出取得最大值时直线
的最大值,并求出取得最大值时直线![]() 的斜率 .
的斜率 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com