
【题目】已知定义在R上的函数f(x)=2x-![]() .
.
(Ⅰ)若f(x)=![]() ,求x的值;
,求x的值;
(Ⅱ)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
【答案】(1)x=1 (2)[-5,+∞)
【解析】试题分析:(1)先根据绝对值定义分类求解方程,注意2x与![]() 互为倒数 (2)利用平方差公式将不等式化简并分离得m≥-(22t+1),最后根据求-(22t+1)最大值,得实数m的取值范围.
互为倒数 (2)利用平方差公式将不等式化简并分离得m≥-(22t+1),最后根据求-(22t+1)最大值,得实数m的取值范围.
试题解析:解:(Ⅰ)当x<0时,f(x)=0,无解;
当x≥0时,f(x)=2x-![]() ,
,
由2x-![]() =
=![]() ,
,
得2·22x-3·2x-2=0,
将上式看成关于2x的一元二次方程,
解得2x=2或2x=-![]() ,
,
∵2x>0,∴x=1
(Ⅱ)当t∈[1,2]时,2t![]() +m
+m![]() ≥0,
≥0,
即m(22t-1)≥-(24t-1),∵22t-1>0,
∴m≥-(22t+1),
∵t∈[1,2],∴-(22t+1)∈[-17,-5],
故实数m的取值范围是[-5,+∞).


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣∞,+∞)上的奇函数,且f(
是定义在(﹣∞,+∞)上的奇函数,且f( ![]() )=
)= ![]() .
.
(1)求实数a、b,并确定函数f(x)的解析式;
(2)判断f(x)在(﹣1,1)上的单调性,并用定义证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x),其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求h(x)的定义域;
(2)判断h(x)的奇偶性,并说明理由;
(3)若a=log327+log2,求使f(x)>1成立的x的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)对其定义域内的两个实数x1、x2 , 都满足不等式 ![]() ,则称函数f(x)在其定义域内具有性质M.给出下列函数:①
,则称函数f(x)在其定义域内具有性质M.给出下列函数:① ![]() ;②y=x2;③y=2x;④y=log2x.其中具有性质M的是( )
;②y=x2;③y=2x;④y=log2x.其中具有性质M的是( )
A.①④
B.②③
C.③④
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
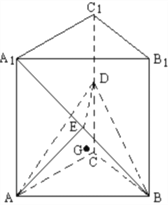
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,D、E分别是
,D、E分别是![]() 与
与![]() 的中点,点E在平面ABD上的射影是
的中点,点E在平面ABD上的射影是![]() 的重心
的重心![]()
(Ⅰ)求![]() 与平面ABD所成角的余弦值
与平面ABD所成角的余弦值
(Ⅱ)求点![]() 到平面
到平面![]() 的距离
的距离
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com