
分析 (1)直接计算可得结论;
(2)求出函数的解析式,再利用三角函数的性质求f(x)的最大值.
解答 解:(1)$f(0)=\frac{{\sqrt{2}}}{2}$.…(2分)
故答案为:$\frac{\sqrt{2}}{2}$.
(2)因为f(x)的最小正周期为π,ω>0,
所以$\frac{2π}{ω}=π$.解得ω=2.
所以$f(x)=sin(2x+\frac{π}{4})$.
因为$0≤x≤\frac{π}{2}$,
所以$\frac{π}{4}≤2x+\frac{π}{4}≤\frac{5π}{4}$.
可得$-\frac{{\sqrt{2}}}{2}≤sin(2x+\frac{π}{4})≤1$.
所以当$x=\frac{π}{8}$时,f(x)的最大值是1.…(5分)
点评 本题考查特殊角三角函数值,考查三角函数的图象与性质,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
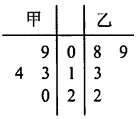 甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )
甲乙两名篮球运动员在4场比赛中的得分情况如图所示.v1,v2分别表示甲、乙二人的平均得分,s1,s2分别表示甲、乙二人得分的方差,那么v1和v2,s1和s2的大小关系是( )| A. | v1>v2,s1>s2 | B. | v1<v2,s1>s2 | C. | v1>v2,s1<s2 | D. | v1<v2,s1<s2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},\sqrt{2})$ | B. | $(0,\sqrt{2})$ | C. | $(-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2})$ | D. | $(\frac{{\sqrt{6}}}{2},\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
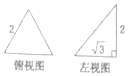 已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )
已知三棱锥的俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一条直角边为2的直角三角形,则该三棱锥的主视图可能为( )| A. | 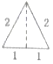 | B. |  | C. | 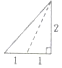 | D. | 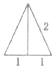 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com