
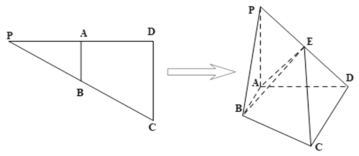
【题目】在四边形ABCD中,BD为四边形的一条对角线,且![]() ,将
,将![]() 沿BD向上翻折,当点A在平面BCD内的投影恰好为
沿BD向上翻折,当点A在平面BCD内的投影恰好为![]() 的外心E时,设直线AE与平面ABC,ACD,ABD的夹角分别为
的外心E时,设直线AE与平面ABC,ACD,ABD的夹角分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题:有厚墙![]() 尺,两只老鼠从墙的两边相对分别打洞穿墙大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问两天后,两鼠间距_______尺,两鼠相遇时,大鼠共穿了______尺墙.
尺,两只老鼠从墙的两边相对分别打洞穿墙大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.问两天后,两鼠间距_______尺,两鼠相遇时,大鼠共穿了______尺墙.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,将
,将![]() 沿
沿![]() 折起,得到四棱锥
折起,得到四棱锥![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)当正视图方向与向量![]() 的方向相同时,此时
的方向相同时,此时![]() 的正视图的面积为
的正视图的面积为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(α为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ=1.
(1)求C1的极坐标方程,并求C1与C2交点的极坐标![]() ;
;
(2)若曲线C3:θ=β(ρ>0)与C1,C2的交点分别为M,N,求|OM||ON|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com