
【题目】如图,在四棱柱![]() 中,
中,![]() ,
,![]() ,且
,且![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)由平行四边形的性质可得![]() ,再根据线面平行的判定定理可得
,再根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)根据题意可知四边形
;(2)根据题意可知四边形![]() 为菱形,进而得到对角线相互垂直,可得
为菱形,进而得到对角线相互垂直,可得![]() ,结合
,结合![]() ,根据线面垂直的判定定理可得到
,根据线面垂直的判定定理可得到![]() 平面
平面![]() .
.
试题解析:(1)解:∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
∴![]() 平面
平面![]() ;
;
(2)解:在四棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
∵![]() ,∴四边形
,∴四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
【方法点晴】本题主要考查棱柱的性质、线面垂直、线面平行的判定定理,属于难题. 解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形且AA1⊥面ABC,F、F1分别是AC,A1C1的中点.

求证:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数x≤3;②标准差s≤2;③平均数x≤3且标准差s≤2;④平均数x≤3且极差小于或等于2;⑤众数等于1且极差小于或等于4.
A. ①② B. ③④ C. ③④⑤ D. ④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示的圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形的圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.

乙商场:从装有2个白球、2个蓝球和2个红球(这些球除颜色外完全相同)的盒子中一次性摸出2球,若摸到的是2个相同颜色的球,则为中奖.
试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿千瓦时)与(x﹣0.4)元成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价﹣成本价)].
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,解方程
时,解方程![]() ;
;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(3)若a为常数,且函数![]() 在区间
在区间![]() 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20,则a的估计值是( )
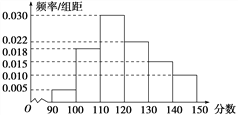
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足对任意
,如果满足对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]()
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界,已知函数
的上界,已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,判断函数
上的值域,判断函数![]() 在
在![]() 上是否为有界函数,并说明理由.
上是否为有界函数,并说明理由.
(2)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第4次为止如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9.求在一年内李明参加驾照考试次数ξ的分布列和ξ的期望,并求李明在一所内领到驾照的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com