
【题目】对于数列![]() ,定义“
,定义“![]() 变换”:
变换”:![]() 将数列
将数列![]() 变换成数列
变换成数列![]() ,其中
,其中![]() ,且
,且![]() ,这种“
,这种“![]() 变换”记作
变换”记作![]() .继续对数列
.继续对数列![]() 进行“
进行“![]() 变换”,得到数列
变换”,得到数列![]() ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为![]() 时变换结束.
时变换结束.
(1)试问![]() 和
和![]() 经过不断的“
经过不断的“![]() 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“![]() 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(2)求![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;
(3)证明:![]() 一定能经过有限次“
一定能经过有限次“![]() 变换”后结束.
变换”后结束.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)根据定义,可得![]() 不能结束,数列
不能结束,数列![]() 能结束,并可写出数列;(2)
能结束,并可写出数列;(2)![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件
变换”后能够结束的充要条件![]() ,先证明
,先证明![]() ,则经过一次“
,则经过一次“![]() 变换”,就得到数列
变换”,就得到数列![]() ,从而结束,再证明命题“若数列
,从而结束,再证明命题“若数列![]() 为常数列,则
为常数列,则![]() 为常数列”, 即可得解;(3)先证明引理:“将数
为常数列”, 即可得解;(3)先证明引理:“将数![]() 的最大项一定不大于数列
的最大项一定不大于数列![]() 的最大项,其中
的最大项,其中
![]() ” ,再分类讨论:第一类是没有为
” ,再分类讨论:第一类是没有为![]() 的项,或者为
的项,或者为![]() 的项与最大项不相邻,(规定首项与末项相邻),此时由引理可知,
的项与最大项不相邻,(规定首项与末项相邻),此时由引理可知,![]() ,第二类是含有为
,第二类是含有为![]() 的项,且与最大项相邻,此时
的项,且与最大项相邻,此时![]() ,证明第二类数列
,证明第二类数列![]() 经过有限次“
经过有限次“![]() 变换”,一定可以得到第一类数列.
变换”,一定可以得到第一类数列.
(1)数列![]() 不能结束,各数列依次为
不能结束,各数列依次为![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;….从而以下重复出现,不会出现所有项均为
;….从而以下重复出现,不会出现所有项均为![]() 的情形.
的情形.
数列![]() 能结束,各数列依次为
能结束,各数列依次为![]() ;
;![]() ;
;![]() ;
;![]() .
.
(2)解:![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件是
变换”后能够结束的充要条件是![]() .
.
若![]() ,则经过一次“
,则经过一次“![]() 变换”就得到数列
变换”就得到数列![]() ,从而结束.
,从而结束.
当数列![]() 经过有限次“
经过有限次“![]() 变换”后能够结束时,先证命题“若数列
变换”后能够结束时,先证命题“若数列![]() 为常数列,则
为常数列,则![]() 为常数列”.
为常数列”.
当![]() 时,数列
时,数列![]() .
.
由数列![]() 为常数列得
为常数列得![]() ,解得
,解得![]() ,从而数列
,从而数列![]() 也为常数列.
也为常数列.
其它情形同理,得证.
在数列![]() 经过有限次“
经过有限次“![]() 变换”后结束时,得到数列
变换”后结束时,得到数列![]() (常数列),由以上命题,它变换之前的数列也为常数列,可知数列
(常数列),由以上命题,它变换之前的数列也为常数列,可知数列![]() 也为常数列.
也为常数列.
所以,数列![]() 经过有限次“
经过有限次“![]() 变换”后能够结束的充要条件是
变换”后能够结束的充要条件是![]() .
.
(3)证明:先证明引理:“数列![]() 的最大项一定不大于数列
的最大项一定不大于数列![]() 的最大项,其中
的最大项,其中![]() ”.
”.
证明:记数列![]() 中最大项为
中最大项为![]() ,则
,则![]() .
.
令![]() ,
,![]() ,其中
,其中![]() .
.
因为![]() , 所以
, 所以![]() ,
,
故![]() ,证毕.
,证毕.
现将数列![]() 分为两类.
分为两类.
第一类是没有为![]() 的项,或者为
的项,或者为![]() 的项与最大项不相邻(规定首项与末项相邻),此时由引理可知,
的项与最大项不相邻(规定首项与末项相邻),此时由引理可知,![]() .
.
第二类是含有为![]() 的项,且与最大项相邻,此时
的项,且与最大项相邻,此时![]() .
.
下面证明第二类数列![]() 经过有限次“
经过有限次“![]() 变换”,一定可以得到第一类数列.
变换”,一定可以得到第一类数列.
不妨令数列![]() 的第一项为
的第一项为![]() ,第二项
,第二项![]() 最大(
最大(![]() ).(其它情形同理)
).(其它情形同理)
①当数列![]() 中只有一项为
中只有一项为![]() 时,
时,
若![]() (
(![]() ),则
),则![]() ,此数列各项均不为
,此数列各项均不为![]() 或含有
或含有![]() 项但与最大项不相邻,为第一类数列;
项但与最大项不相邻,为第一类数列;
若![]() ,则
,则![]() ;
;![]() 此数列各项均不为
此数列各项均不为![]() 或含有
或含有![]() 项但与最大项不相邻,为第一类数列;
项但与最大项不相邻,为第一类数列;
若![]() (
(![]() ),则
),则![]() ,此数列各项均不为
,此数列各项均不为![]() ,为第一类数列;
,为第一类数列;
若![]() ,则
,则![]() ;
;![]() ;
;![]() ,
,
此数列各项均不为![]() ,为第一类数列.
,为第一类数列.
②当数列![]() 中有两项为
中有两项为![]() 时,若
时,若![]() (
(![]() ),则
),则![]() ,此数列各项均不为
,此数列各项均不为![]() ,为第一类数列;
,为第一类数列;
若![]() (
(![]() ),则
),则![]() ,
,![]() ,此数列各项均不为
,此数列各项均不为![]() 或含有
或含有![]() 项但与最大项不相邻,为第一类数列.
项但与最大项不相邻,为第一类数列.
③当数列![]() 中有三项为
中有三项为![]() 时,只能是
时,只能是![]() ,则
,则![]() ,
,
![]() ,
,![]() ,此数列各项均不为
,此数列各项均不为![]() ,为第一类数列.
,为第一类数列.
总之,第二类数列![]() 至多经过
至多经过![]() 次“
次“![]() 变换”,就会得到第一类数列,即至多连续经历
变换”,就会得到第一类数列,即至多连续经历![]() 次“
次“![]() 变换”,数列的最大项又开始减少.
变换”,数列的最大项又开始减少.
又因为各数列的最大项是非负整数,
故经过有限次“![]() 变换”后,数列的最大项一定会为
变换”后,数列的最大项一定会为![]() ,此时数列的各项均为
,此时数列的各项均为![]() ,从而结束.
,从而结束.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组,![]() 年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者.
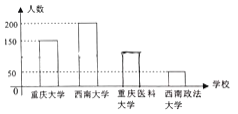
(1)分别求出从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数;
(2)若“嘉宾”小组的2名志愿者只能从重庆医科大学或西南政法大学抽出,求这2人分别来自不同大学的概率(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国国际智能产业博览会(智博会)每年在重庆市举办一届,每年参加服务的志愿者分“嘉宾”、“法医”等若干小组.2018年底,来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”,如图是四所大学参加培训人数的不完整条形统计图,现用分层抽样的方法从中抽出50人作为2019年中国国际智博会服务的志愿者.
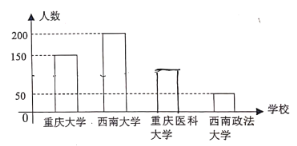
(1)若“嘉宾”小组需要2名志愿者,求这2人分别来自不同大学的概率(结果用分数表示).
(2)若法医小组的3名志愿者只能从重庆医科大学或西南政法大学抽出,用5表示抽出志愿者来自重庆医科大学的人数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 对任意实数
对任意实数![]() ,
,![]() 满足:
满足:![]() ,且
,且![]() ,
,![]() ,并且当
,并且当![]() 时,
时,![]() .给出如下结论:①函数
.给出如下结论:①函数![]() 是偶函数;②函数
是偶函数;②函数![]() 在
在![]() 上单调递增;③函数
上单调递增;③函数![]() 是以2为周期的周期函数;④
是以2为周期的周期函数;④![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为减轻汽车尾气对大气的污染,保卫蓝天,鼓励广大市民使用电动交通工具出行,决定为电动车(含电动自行车和电动汽车)免费提供电池检测服务.现从全市已挂牌照的![]() 电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
电动车中随机抽取100辆委托专业机构免费为它们进行电池性能检测,电池性能分为需要更换、尚能使用、较好、良好四个等级,并分成电动自行车和电动汽车两个群体分别进行统计,样本分布如图.
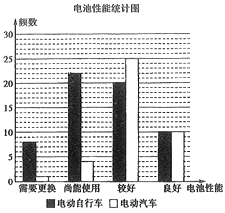
(1)采用分层抽样的方法从电池性能较好的电动车中随机抽取9辆,再从这9辆中随机抽取2辆,求至少有一辆为电动汽车的概率;
(2)为进一步提高市民对电动车的使用热情,市政府准备为电动车车主一次性发放补助,标准如下:①电动自行车每辆补助300元;②电动汽车每辆补助500元;③对电池需要更换的电动车每辆额外补助400元.试求抽取的100辆电动车执行此方案的预算;并利用样本估计总体,试估计市政府执行此方案的预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 为原正三棱柱的底面,
为原正三棱柱的底面,![]() ,点D为
,点D为![]() 的中点.
的中点.
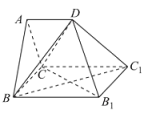
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com