解:(Ⅰ)设P(x,y),则由直线PA与直线PB斜率之积为-

,得
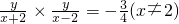
.
整理得曲线C的方程为
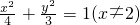
.----(4分)
(Ⅱ)若|

-

|=|

+

|,则
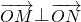
.
设M(x
1,y
1),N(x
2,y
2).
若直线MN斜率不存在,则N(x
1,-y
1).
由
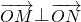
得
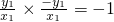
,又
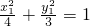
,∴
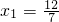
.
∴直线MN方程为
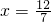
.
∴原点O到直线MN的距离d=
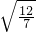
.----(6分)
若直线MN斜率存在,设方程为y=kx+m与椭圆方程联立,消去y可得(4k
2+3)x
2+8kmx+4m
2-12=0.
∴x
1+x
2=
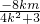
,x
1x
2=
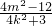
.(*)----(8分)
由
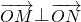
得

,整理得(k
2+1)x
1x
2+km(x
1+x
2)+m
2=0.
(*)式代入:(k
2+1)×
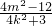
+km×
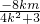
+m
2=0
解得7m
2=12(k
2+1).----(10分)
此时原点O到直线MN的距离d=
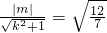
.
故原点O到直线MN的距离恒为d=
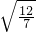
.
∴存在以原点为圆心且与MN总相切的圆,方程为
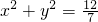
.----(12分)
分析:(Ⅰ)设P(x,y),则由直线PA与直线PB斜率之积为-

,建立等式,即可求曲线C的方程;
(Ⅱ)若|

-

|=|

+

|,则
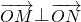
.分斜率存在与不存在,结合椭圆的方程,利用韦达定理,可得原点O到直线MN的距离恒为d=
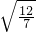
,从而存在以原点为圆心且与MN总相切的圆.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,正确运用韦达定理是关键.

 ,记点P的轨迹为曲线C.
,记点P的轨迹为曲线C. -
- |-|
|-| +
+ |,是否存在以原点为圆心且与MN总相切的圆?若存在,求出该圆的方程;若不存在,请说明理由.
|,是否存在以原点为圆心且与MN总相切的圆?若存在,求出该圆的方程;若不存在,请说明理由. ,得
,得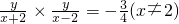 .
.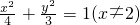 .----(4分)
.----(4分) -
- |=|
|=| +
+ |,则
|,则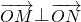 .
.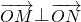 得
得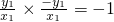 ,又
,又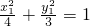 ,∴
,∴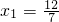 .
.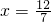 .
.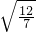 .----(6分)
.----(6分)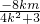 ,x1x2=
,x1x2=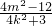 .(*)----(8分)
.(*)----(8分)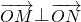 得
得 ,整理得(k2+1)x1x2+km(x1+x2)+m2=0.
,整理得(k2+1)x1x2+km(x1+x2)+m2=0.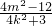 +km×
+km×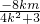 +m2=0
+m2=0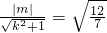 .
.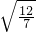 .
.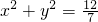 .----(12分)
.----(12分) ,建立等式,即可求曲线C的方程;
,建立等式,即可求曲线C的方程; -
- |=|
|=| +
+ |,则
|,则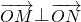 .分斜率存在与不存在,结合椭圆的方程,利用韦达定理,可得原点O到直线MN的距离恒为d=
.分斜率存在与不存在,结合椭圆的方程,利用韦达定理,可得原点O到直线MN的距离恒为d=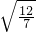 ,从而存在以原点为圆心且与MN总相切的圆.
,从而存在以原点为圆心且与MN总相切的圆.
