
ЁОЬтФПЁПФГбЇаЃдквЛДЮЕкЖўПЮЬУЛюЖЏжаЃЌЬивтЩшжУСЫЙ§ЙижЧСІгЮЯЗЃЌгЮЯЗЙВЮхЙиЃЎЙцЖЈЕквЛЙиУЛЙ§епУЛНБРјЃЌЙ§![]()
![]() ЙиепНБРј
ЙиепНБРј![]() МўаЁНБЦЗЃЈНБЦЗЖМвЛбљЃЉЃЎЯТЭМЪЧаЁУїдк10ДЮЙ§ЙигЮЯЗжаЙ§ЙиЪ§ЕФЬѕаЮЭМЃЌвдДЫЦЕТЪЙРМЦИХТЪЃЎ
МўаЁНБЦЗЃЈНБЦЗЖМвЛбљЃЉЃЎЯТЭМЪЧаЁУїдк10ДЮЙ§ЙигЮЯЗжаЙ§ЙиЪ§ЕФЬѕаЮЭМЃЌвдДЫЦЕТЪЙРМЦИХТЪЃЎ
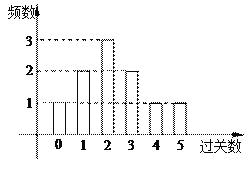
(Ђё)ЙРМЦаЁУїдк1ДЮгЮЯЗжаЫљЕУНБЦЗЪ§ЕФЦкЭћжЕЃЛ
(Ђђ)ЙРМЦаЁУїдк3 ДЮгЮЯЗжажСЩйЙ§СНЙиЕФЦНОљДЮЪ§ЃЛ
(Ђѓ)ЙРМЦаЁУїдк3 ДЮгЮЯЗжаЫљЕУНБЦЗГЌЙ§30МўЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ4ЃЛЃЈ2ЃЉ2.1ЃЛЃЈ3ЃЉ0.031
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСаГіаЁУїдк1ДЮгЮЯЗжаЫљЕУНБЦЗЪ§ЮЊ![]() ЕФЗжВМСаЃЌИљОнЗжВМСаЧѓГіЦкЭћМДПЩЃЛЃЈ2ЃЉгЩБэПЩЕУаЁУїдк1 ДЮгЮЯЗжажСЩйЙ§СНЙиЕФИХТЪЮЊ0.7ЃЌгЩЖўЯюЗжВМПЩЕУНсЙћЃЛЃЈ3ЃЉЗжЮіПЩЕУаЁУїдк3 ДЮгЮЯЗжаЫљЕУНБЦЗГЌЙ§30МўКЌШ§РрЃКЧЁКУвЛДЮ
ЕФЗжВМСаЃЌИљОнЗжВМСаЧѓГіЦкЭћМДПЩЃЛЃЈ2ЃЉгЩБэПЩЕУаЁУїдк1 ДЮгЮЯЗжажСЩйЙ§СНЙиЕФИХТЪЮЊ0.7ЃЌгЩЖўЯюЗжВМПЩЕУНсЙћЃЛЃЈ3ЃЉЗжЮіПЩЕУаЁУїдк3 ДЮгЮЯЗжаЫљЕУНБЦЗГЌЙ§30МўКЌШ§РрЃКЧЁКУвЛДЮ![]() КЭСНДЮ
КЭСНДЮ![]() ЃЌЧЁКУЖўДЮ
ЃЌЧЁКУЖўДЮ![]() ЃЌЧЁКУШ§ДЮ
ЃЌЧЁКУШ§ДЮ![]() ЃЌгЩЛЅГтЪТМўМАЯрЛЅЖРСЂЪТМўЗЂЩњЕФИХТЪПЩЕУНсЙћ.
ЃЌгЩЛЅГтЪТМўМАЯрЛЅЖРСЂЪТМўЗЂЩњЕФИХТЪПЩЕУНсЙћ.
ЪдЬтНтЮіЃК (1)ЩшаЁУїдк1ДЮгЮЯЗжаЫљЕУНБЦЗЪ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 4 | 8 | 16 |
P | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
![]() ЕФЦкЭћжЕ
ЕФЦкЭћжЕ![]() ЃЛ
ЃЛ
(2)аЁУїдк1 ДЮгЮЯЗжажСЩйЙ§СНЙиЕФИХТЪЮЊ0.7ЃЌ
ЩшаЁУїдк3 ДЮгЮЯЗжажСЩйЙ§СНЙиЕФДЮЪ§ЮЊXЃЌПЩжЊ![]() ЃЌ
ЃЌ
дђXЕФЦНОљДЮЪ§![]() ЃЛ
ЃЛ
(3)аЁУїдк3 ДЮгЮЯЗжаЫљЕУНБЦЗГЌЙ§30МўКЌШ§РрЃКЧЁКУвЛДЮ![]() КЭСНДЮ
КЭСНДЮ![]() ЃЌЧЁКУЖўДЮ
ЃЌЧЁКУЖўДЮ![]() ЃЌЧЁКУШ§ДЮ
ЃЌЧЁКУШ§ДЮ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() =
=![]() ЃЌ
ЃЌ
![]()
ЫљвдаЁУїдк3 ДЮгЮЯЗжаЫљЕУНБЦЗГЌЙ§30МўЕФИХТЪЮЊ![]() ЃЎ
ЃЎ


 НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ
НђЧХНЬг§МЦЫуаЁзДдЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌЗжБ№ЪЧЭждВ
ЃЌЗжБ№ЪЧЭждВ![]() ЕФзѓЁЂгвНЙЕу.
ЕФзѓЁЂгвНЙЕу.
ЃЈ1ЃЉШєЕу![]() ЪЧЕквЛЯѓЯоФкЭждВЩЯЕФвЛЕуЃЌ
ЪЧЕквЛЯѓЯоФкЭждВЩЯЕФвЛЕуЃЌ ![]() ,ЧѓЕу
,ЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉЩшЙ§ЖЈЕу![]() ЕФжБЯп
ЕФжБЯп![]() гыЭждВНЛгкВЛЭЌЕФСНЕу
гыЭждВНЛгкВЛЭЌЕФСНЕу![]() ЃЌЧв
ЃЌЧв![]() ЮЊШёНЧЃЈЦфжа
ЮЊШёНЧЃЈЦфжа![]() ЮЊзјБъдЕуЃЉЃЌЧѓжБЯп
ЮЊзјБъдЕуЃЉЃЌЧѓжБЯп![]() ЕФаБТЪ
ЕФаБТЪ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊУнКЏЪ§fЃЈxЃЉ=xЉm2+m+2ЃЈmЁЪZЃЉдкЃЈ0ЃЌ+ЁоЃЉЩЯЕЅЕїЕндіЃЎ
ЃЈ1ЃЉЧѓКЏЪ§fЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшgЃЈxЃЉ=fЃЈxЃЉЉax+1ЃЌaЮЊЪЕГЃЪ§ЃЌЧѓgЃЈxЃЉдкЧјМф[Љ1ЃЌ1]ЩЯЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдВCОЙ§Еу![]() ЃЌЧвдВаФ
ЃЌЧвдВаФ![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌгжжБЯп
ЩЯЃЌгжжБЯп![]() гыдВCНЛгкP,QСНЕу.
гыдВCНЛгкP,QСНЕу.
ЃЈ1ЃЉЧѓдВCЕФЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)Й§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌЧв
ЃЌЧв![]() НЛдВCгкM,NСНЕуЃЌЧѓЫФБпаЮ
НЛдВCгкM,NСНЕуЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЕФзюДѓжЕ.
ЕФУцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() ЃЌдВ
ЃЌдВ![]()
ЃЈ1ЃЉЙ§Еу![]() ЕФдВЕФЧаЯпжЛгавЛЬѕЃЌЧѓ
ЕФдВЕФЧаЯпжЛгавЛЬѕЃЌЧѓ![]() ЕФжЕМАЧаЯпЗНГЬЃЛ
ЕФжЕМАЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШєЙ§Еу![]() ЧвдкСНзјБъжсЩЯНиОрЯрЕШЕФжБЯпБЛдВНиЕУЕФЯвГЄЮЊ
ЧвдкСНзјБъжсЩЯНиОрЯрЕШЕФжБЯпБЛдВНиЕУЕФЯвГЄЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() ЯрЧаЃЌЧвгы
ЯрЧаЃЌЧвгы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() .ШєЖЏЕу
.ШєЖЏЕу![]() гыСНЖЈЕу
гыСНЖЈЕу![]() ЫљЙЙГЩШ§НЧаЮЕФжмГЄЮЊ6ЃЎ
ЫљЙЙГЩШ§НЧаЮЕФжмГЄЮЊ6ЃЎ
(Ђё) ЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
(Ђђ) ЩшаБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() НЛЧњЯп
НЛЧњЯп![]() гк
гк![]() СНЕуЃЌЕБ
СНЕуЃЌЕБ![]() ЃЌЧв
ЃЌЧв![]() ЮЛгкжБЯп
ЮЛгкжБЯп![]() ЕФСНВрЪБЃЌжЄУїЃК
ЕФСНВрЪБЃЌжЄУїЃК ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌаБТЪЮЊ
ЃЌаБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() Й§Еу
Й§Еу![]() ЃЌЧв
ЃЌЧв![]() КЭвд
КЭвд![]() ЮЊдВ
ЮЊдВ![]() ЯрЧа.
ЯрЧа.
ЃЈ1ЃЉЧѓдВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉдкдВ![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌШєДцдкЃЌЧѓГіЫљгаЕФЕу
ЃЌШєДцдкЃЌЧѓГіЫљгаЕФЕу![]() ЕФзјБъЃЛШєВЛДцдкЫЕУїРэгЩЃЛ
ЕФзјБъЃЛШєВЛДцдкЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєВЛЙ§![]() ЕФжБЯп
ЕФжБЯп![]() гыдВ
гыдВ![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ ![]() СНЕуЃЌЧвТњзу
СНЕуЃЌЧвТњзу![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФаБТЪвРДЮЮЊЕШБШЪ§СаЃЌЧѓжБЯп
ЕФаБТЪвРДЮЮЊЕШБШЪ§СаЃЌЧѓжБЯп![]() ЕФаБТЪ.
ЕФаБТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБШ§РтжљABCЉA1B1C1жаЃЌШєЁЯBAC=90ЁуЃЌAB=AC=AA1 ЃЌ дђвьУцжБЯпBA1гыAC1ЫљГЩЕФНЧЕШгкЃЈЁЁЁЁЃЉ
A.30Ёу
B.45Ёу
C.60Ёу
D.90Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЏдВ![]() гыдВ
гыдВ![]() ЭтЧаЃЌгыдВ
ЭтЧаЃЌгыдВ![]() ФкЧа.
ФкЧа.
ЃЈЂёЃЉЪдЧѓЖЏдВдВаФЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈЂђЃЉгыдВ![]() ЯрЧаЕФжБЯп
ЯрЧаЕФжБЯп![]() гыЙьМЃ
гыЙьМЃ![]() НЛгк
НЛгк![]() СНЕуЃЌШєжБЯп
СНЕуЃЌШєжБЯп![]() ЕФаБТЪГЩЕШБШЪ§СаЃЌЪдЧѓжБЯп
ЕФаБТЪГЩЕШБШЪ§СаЃЌЪдЧѓжБЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com