
【题目】已知集合M={1,2,3,4,5,6,7,8,9,10,11,12},以下命题正确的序号是 .
①如果函数f(x)=x(x﹣a1)(x﹣a2)…(x﹣a7),其中ai∈M(i=1,2,3,…,7),那么f′(0)的最大值为127 .
②数列{an}满足首项a1=2,ak+12﹣ak2=2,k∈N* , 当n∈M且n最大时,数列{an}有2048个.
③数列{an}(n=1,2,3,…,8)满足a1=5,a8=7,|ak+1﹣ak|=2,k∈N* , 如果数列{an}中的每一项都是集合M的元素,则符合这些条件的不同数列{an}一共有33个.
④已知直线amx+any+ak=0,其中am , an , ak∈M,而且am<an<ak , 则一共可以得到不同的直线196条.
【答案】②③
【解析】解:对于①,令g(x)=(x﹣a1)(x﹣a2)…(x﹣an),
则f′(x)=g(x)+xg′(x),
∵f(x)=x(x﹣a1)(x﹣a2)…(x﹣a7),
∴f′(0)=g(0)=(﹣a1)(﹣a2)…(﹣a7)<(﹣1)7=﹣1.命题①错误;
对于②,n=12,令 ![]() ,则bk+1﹣bk=2,b1=4.
,则bk+1﹣bk=2,b1=4.
对于每一个ai(i>1)都有两种取值,共211=2048个.命题②正确;
对于③,这个问题相当于走楼梯问题,一共六级楼梯,可以进一步也可以退一步,
现在在第三级,求走7步后到第四级楼梯的走法.
事实上,必定要向前走四步和向后走三步,共 ![]() 种走法,但先走四步和先退三步这两种都是不行的.
种走法,但先走四步和先退三步这两种都是不行的.
∴共33种走法,即符合条件的不同数列{an}一共有33个.命题③正确;
对于④,考虑满足am<an<ak(am , an , ak)数组的数量,共 ![]() 个.
个.
而数组
(1,2,3),(2,4,6),
(3,6,9),(4,8,12),
(1,2,4),(2,4,8),
(3,6,12),(1,2,5),
(2,4,10),(1,2,6),
(2,4,12),(1,3,4),
(2,6,8),(3,9,12),
(1,3,5),(2,6,10),
(1,3,6),(2,6,12),
(1,4,5),(2,8,10),
(1,4,6),(2,8,12),
(1,5,6),(2,10,12),
(2,3,4),(4,6,8),
(6,9,12),(2,3,5),
(4,6,10),(2,3,6),
(4,6,12),(2,4,5),
(4,8,10),(2,4,6),
(4,8,12),(2,5,6),
(4,10,12),(3,4,5),
(6,8,10),(3,4,6),
(6,8,12),(3,5,6),
(6,10,12),(4,5,6),
(8,10,12)中共重复25个数组,
∴一共可以得到不同的直线195条.
命题④错误.
所以答案是:②③.
【考点精析】通过灵活运用命题的真假判断与应用,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x2﹣bx)(b∈R)在区间[ ![]() ,2]上存在单调递增区间,则实数b的取值范围是( )
,2]上存在单调递增区间,则实数b的取值范围是( )
A.(﹣∞, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列函数:
①y=x+ ![]() ;
;
②y=lgx+logx10(x>0,x≠1);
③y=sinx+ ![]() (0<x≤
(0<x≤ ![]() );
);
④y= ![]() ;
;
⑤y= ![]() (x+
(x+ ![]() )(x>2).
)(x>2).
其中最小值为2的函数序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax﹣a﹣x+2(a>0,且a≠1),若g(2)=a,则f(2)的值为(
A.![]()
B.2
C.![]()
D.a2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少? 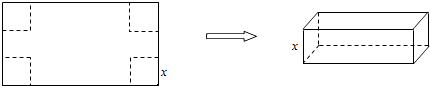
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数y= ![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②若lna<1成立,则a的取值范围是(﹣∞,e);
③函数f(x)=ax+1﹣2(a>0,a≠1)的图象过定点(﹣1,﹣1);
④方程x2+(a﹣3)x+a=0的有一个正实根,一个负实根,则a<0;
⑤函数f(x)=loga(6﹣ax)(a>0,a≠1)在[0,2]上为减函数,则1<a<3.
其中正确的个数( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:实数x满足x2﹣4ax+3a2<0,其中a>0; q:实数x满足2<x≤3.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com