练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形，由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形，沿三角形的三边中点连线，将它分成4个小三角形，去掉中间的那一个小三角形后，对其余3个小三角形重复上述过程逐次得到各个图形，如上图.现在图（3）中随机选取一个点，则此点取自阴影部分的概率为________

    【答案】

    【解析】

    由归纳推理得：设图（3）中1个小阴影三角形的面积为，则图（3）中阴影部分的面积为：，又图（3）中大三角形的面积为，由几何概型的概率公式计算可得；

    解：设图（3）中1个小阴影三角形的面积为，

    则图（3）中阴影部分的面积为：，

    又图（3）中大三角形的面积为，

    由几何概型中的面积型可得：

    此点取自阴影部分的概率为，

    故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，设点，定义，其中为坐标原点，对于下列结论：

    符合的点的轨迹围成的图形面积为8；

    设点是直线：上任意一点，则；

    设点是直线：上任意一点，则使得“最小的点有无数个”的充要条件是；

    设点是椭圆上任意一点，则．

    其中正确的结论序号为　　

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，平面ABCD，为等边三角形，，，M为AC的中点．

    证明：平面PCD；

    若PD与平面PAC所成角的正切值为，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：的左焦点为，且点在C上．

    求C的方程；

    设点P关于x轴的对称点为点不经过P点且斜率为的直线1与C交于A，B两点，直线PA，PB分别与x轴交于点M，N，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某运动会将在深圳举行，组委会招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位：），身高在以上（包括）定义为“高个子”，身高在以下（不包括）定义为“非高个子”．

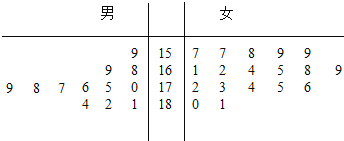
    （1）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率；

    （2）若从身高以上（包括）的志愿者中选出男、女各一人，设这2人身高相差（），求的分布列和数学期望（均值）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4 坐标系与参数方程选讲

    在直角坐标系中，直线的参数方程（为参数），以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，曲线极坐标方程为.

    （1）求直线的普通方程以及曲线的参数方程；

    （2）当时，为曲线上动点，求点到直线距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知图形ABCDEF，内部连有线段.

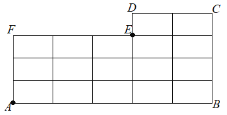
    （1）由点A沿着图中的线段到达点E的最近路线有多少条？

    （2）由点A沿着图中的线段到达点C的最近路线有多少条？

    （3）求出图中总计有多少个矩形？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象关于原点对称，其中为常数.

    （1）求的值；

    （2）当时， 恒成立，求实数的取值范围；

    （3）若关于的方程在上有解，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数、，下列命题中正确的是（ ）

    A.不等式的解集为

    B.函数在上单调递增，在上单调递减

    C.若函数有两个极值点，则

    D.若时，总有恒成立，则

    查看答案和解析>>

    同步练习册答案