练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    试判断函数在[，+∞）上的单调性．

    单调递增

    解析试题分析：因为函数.所以由函数的单调性的定义来判断函数的单调性.通过自变量的大小的变化从而得到函数值的的大小变化.本小题关键是的正负的判断.由于.所以可得>0.本小题也可以通过求导数来证明.
    试题解析：设，则有=
    ===．
    ，且，，
    所以，即．所以函数在区间[，+∞)上单调递增．
    考点：1.函数的单调性的证明.2.函数值的大小比较.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    已知函数．
    （1）判断函数的奇偶性并证明；
    （2）当时，求函数的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数.
    （1）若的定义域和值域均是，求实数的值；
    （2）若在区间上是减函数，且对任意的，都有，求实数的取值范围；
    （3）若，且对任意的，都存在，使得成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数（）
    （Ⅰ）若函数是定义在R上的偶函数，求a的值；
    （Ⅱ）若不等式对任意，恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测：服药后每毫升血液中的含药量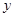（单位：微克）与时间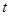（单位：小时）之间近似满足如图所示的曲线．

    （Ⅰ）写出第一次服药后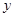与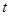之间的函数关系式；
    （Ⅱ）据进一步测定：每毫升血液中含药量不少于微克时，治疗有效．问：服药多少小时开始有治疗效果？治疗效果能持续多少小时？（精确到0．1）（参考数据：）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝log4(4x＋1)＋kx(k∈R)是偶函数．
    (1)求k的值；
    (2)探究函数f(x)＝ax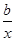＋(a、b是正常数)在区间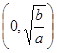和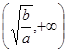上的单调性（只需写出结论，不要求证明）.并利用所得结论，求使方程f(x)－log4m＝0有解的m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设函数f(x)=|2x-1|+|2x-3|,x∈R
    (Ⅰ)解不等式f(x)≤5；
    (Ⅱ)若的定义域为R，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下，大桥上的车流速度v（单位：千米/小时）是车流密度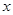（单位：辆/千米）的函数.当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时，研究表明：当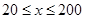时，车流速度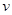是车流密度x的一次函数．
    （1）当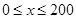时，求函数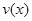的表达式；
    （2）当车流密度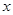为多大时，车流量（单位时间内通过桥上某观点的车辆数，单位：辆/每小时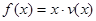）可以达到最大，并求出最大值（精确到1辆/小时）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在上最大值是5，最小值是2，若，在上是单调函数，求m的取值范围.

    查看答案和解析>>

    同步练习册答案