
(09年长郡中学一模文)(12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.

解析:方法一:
(I)证明:连结OC
![]() ………1分
………1分
![]()
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]() ……………3分
……………3分
又![]()
![]() 平面
平面![]() ……………4分
……………4分
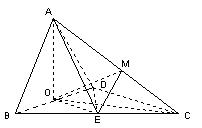
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知![]()
![]() 直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………5分
直线OE与EM所成的锐角就是异面直线AB与CD所成的角。……………5分
在![]() 中,
中,
![]() ……………6分
……………6分
![]() 是直角
是直角![]() 斜边AC上的中线,
斜边AC上的中线,
![]() ……………7分
……………7分
![]()
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………8分
;……………8分
(III)解:设点E到平面ACD的距离为![]()
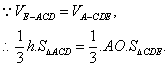 ……………9分
……………9分
在![]() 中,
中,![]()
![]() ……………10分
……………10分
而![]() ……………11分
……………11分
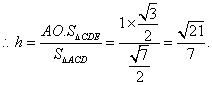
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]() ……………12分
……………12分
方法二:
(I)同方法一.……………4分
(II)解:以O为原点,如图建立空间直角坐标系,

则![]()
![]() ………………6分
………………6分
![]() …………7分
…………7分
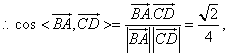 ………9分
………9分
![]() 异面直线AB与CD所成角大小的余弦为
异面直线AB与CD所成角大小的余弦为![]() ;……………8分
;……………8分
(III)解:设平面ACD的法向量为![]() 则
则
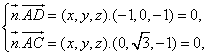 ……………9分
……………9分
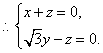
令![]() 得
得![]() 是平面ACD的一个法向量.……………10分
是平面ACD的一个法向量.……………10分
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
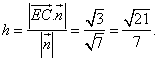 ……………12分
……………12分


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
(09年长郡中学一模文)(13分)
由函数![]() 确定数列
确定数列![]() ,
,![]() ,函数
,函数![]() 的反函数
的反函数![]() 能确定数列
能确定数列![]() ,
,![]() ,若对于任意
,若对于任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 是数列
是数列![]() 的“自反函数列”.
的“自反函数列”.
(I)设函数![]() ,若由函数
,若由函数![]() 确定的数列
确定的数列![]() 的自反数列为
的自反数列为![]() ,求
,求![]() ;
;
(Ⅱ)已知正数数列![]() 的前n项和
的前n项和 ,写出
,写出![]() 表达式,并证明你的结论;
表达式,并证明你的结论;
(Ⅲ)在(I)和(Ⅱ)的条件下,![]() ,当
,当![]() 时,设
时,设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,且
项和,且![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长郡中学一模文)(13分)
若实数a≠0,函数查看答案和解析>>
科目:高中数学 来源: 题型:
(09年长郡中学一模文)(13分)
已知圆![]() ,定点
,定点![]() ,点
,点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 上,点
上,点
![]() 在
在![]() 上,且满足
上,且满足![]()
(I)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com