
【题目】如图所示,将![]() 方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )
方格纸中每个小方格染三种颜色之一,使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同,称他们的公共边为“分割边”,则分割边条数的最小值为( )

A.33B.56C.64D.78
【答案】B
【解析】
记分隔边的条数为![]() ,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,将方格的行从上至下依次记为
,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,将方格的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含有
为含有![]() 色方格的行数与列数之和,定义当
色方格的行数与列数之和,定义当![]() 行含有
行含有![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,计算得到
,计算得到![]() ,再证明
,再证明![]() ,再证明对任意
,再证明对任意![]() 均有
均有![]() ,最后求出分隔边条数的最小值.
,最后求出分隔边条数的最小值.
记分隔边的条数为![]() ,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,
,首先将方格按照按图分三个区域,分别染成三种颜色,粗线上均为分隔边,
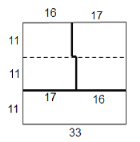
此时共有56条分隔边,即![]() ,
,
其次证明:![]() ,
,
将将方格的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() ,行
,行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() ,三种颜色分别记为
,三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() ,设
,设![]() 为含有
为含有![]() 色方格的行数与列数之和,定义当
色方格的行数与列数之和,定义当![]() 行含有
行含有![]() 色方格时,
色方格时,![]() ,否则
,否则![]() ,类似的定义
,类似的定义![]() ,
,
所以![]() ,
,
由于染![]() 色的格有
色的格有![]() 个,设含有
个,设含有![]() 色方格的行有
色方格的行有![]() 个,列有
个,列有![]() 个,则
个,则![]() 色的方格一定再这个
色的方格一定再这个![]() 行和
行和![]() 列的交叉方格中,
列的交叉方格中,
从而![]() ,
,
所以![]() ①,
①,
由于在行![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
类似的,在列![]() 中有
中有![]() 种颜色的方格,于是至少有
种颜色的方格,于是至少有![]() 条分隔边,
条分隔边,
则![]() ②
②
![]() ③
③
下面分两种情形讨论,
(1)有一行或一列所有方格同色,
不妨设有一行均为![]() 色,则方格的33列均含有
色,则方格的33列均含有![]() 的方格,又
的方格,又![]() 色的方格有363个,故至少有11行有
色的方格有363个,故至少有11行有![]() 色方格,于是
色方格,于是![]() ④
④
由①③④得
![]() ,
,
(2)没有一行也没有一列的所有方格同色,
则对任意![]() 均有
均有![]() ,
,
从而,由式②知:
![]() ,
,
综上,分隔边条数的最小值为56.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() 且满足
且满足![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(2)若方程![]() 有实数根
有实数根![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点,设正数
的一个不动点,设正数![]() 为函数
为函数![]() 的一个不动点,且
的一个不动点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以正四棱锥VABCD的底面中心O为坐标原点建立空间直角坐标系Oxyz,其中Ox∥BC,Oy∥AB,E为VC的中点.正四棱锥的底面边长为2a,高为h,且有cos〈![]() ,
,![]() 〉=-
〉=-![]() .
.
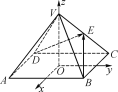
(1)求![]() 的值;
的值;
(2)求二面角B-VC-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() (
(![]() )与
)与![]() 交于两个不同的点
交于两个不同的点![]() 、
、![]() ,且
,且![]() 时直线
时直线![]() 与
与![]() 的两条渐近线所围成的三角形恰为等边三角形.
的两条渐近线所围成的三角形恰为等边三角形.
(1)求双曲线![]() 的方程;
的方程;
(2)若坐标原点![]() 在以线段
在以线段![]() 为直径的圆的内部,求实数
为直径的圆的内部,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 、
、![]() 分别是
分别是![]() 的左、右两顶点,线段
的左、右两顶点,线段![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 在
在![]() 轴上的射影长为定值.
轴上的射影长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为![]() 的数列
的数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)若数列![]() 的通项
的通项![]() 满足
满足![]() ,且
,且![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(2)若数列![]() 的通项
的通项![]() 满足
满足 ,前n项和为
,前n项和为![]() ,当数列
,当数列![]() 是等差数列时,对任意的
是等差数列时,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 构成的集合.
构成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体有五条棱长为3,且外接球半径为2.动点P在四面体的内部或表面,P到四个面的距离之和记为s.已知动点P在![]() ,
,![]() 两处时,s分别取得最小值和最大值,则线段
两处时,s分别取得最小值和最大值,则线段![]() 长度的最小值为______.
长度的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定整数![]() (
(![]() ),设集合
),设集合![]() ,记集合
,记集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() 构成以
构成以![]() 为首项,
为首项,![]() (
(![]() )为公差的等差数列,求证:集合
)为公差的等差数列,求证:集合![]() 中的元素个数为
中的元素个数为![]() ;
;
(3)若![]() 构成以
构成以![]() 为首项,
为首项,![]() 为公比的等比数列,求集合
为公比的等比数列,求集合![]() 中元素的个数及所有元素之和.
中元素的个数及所有元素之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com