
【题目】已知在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆锥曲线C的极坐标方程为p2= ![]() ,定点A(0,﹣
,定点A(0,﹣ ![]() ),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
),F1 , F2是圆锥曲线C的左、右焦点,直线l经过点F1且平行于直线AF2 .
(1)求圆锥曲线C的直角坐标方程和直线l的参数方程;
(2)若直线l与圆锥曲线C交于M,N两点,求|F1M||F1N|.
【答案】
(1)解:∵p2= ![]() ,∴3ρ2+ρ2sin2θ=12.
,∴3ρ2+ρ2sin2θ=12.
∴曲线C的直角坐标方程为3x2+3y2+y2=12,即 ![]() .
.
∴F1(﹣1,0),F2(1,0),
∴直线AF2的斜率 ![]() =
= ![]() =
= ![]() .∴直线l的倾斜角为
.∴直线l的倾斜角为 ![]() .
.
在l上任取一点P,设有向线段F1P的长为t,
则直线l的参数方程为 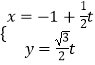 (t为参数).
(t为参数).
(2)解:将l的参数方程代入曲线的直角坐标方程得 ![]() ,即5t2﹣4t﹣12=0.
,即5t2﹣4t﹣12=0.
设M,N对应的参数分别为t1,t2,则t1t2=﹣ ![]() .
.
∴|F1M||F1N|=|t1||t2|=|t1t2|= ![]()
【解析】(1)根据极坐标与直角坐标的对应关系得出曲线C的直角坐标方程,根据焦点坐标计算直线l的倾斜角,令F1到直线l上一点P的有向线段t为参数写出l的参数方程;,(2)将直线l的参数方程代入曲线的直角坐标方程,得出关于t的方程,利用参数得几何意义计算|F1M||F1N|.


科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x≥0时,f(x)=![]() ,则关于x的函数F(x)=f(x)-a(0<a<1,a为常数)的所有零点之和为______.
,则关于x的函数F(x)=f(x)-a(0<a<1,a为常数)的所有零点之和为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定个人稿费缴纳方法为:不超过800元的不纳税,超过800元而不超过4000元的按超过800元部分的14%纳税,超过4000元的按全部稿酬的11.2%纳税(本题中稿费均指纳税前稿费).
(Ⅰ)某人出了一本书,获得30000元的个人稿费,则这个人需要纳税是多少元?
(Ⅱ)试建立某人所得稿费x元与纳税额y元的函数关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项公式为an=﹣2n+p,数列{bn}的通项公式为bn=2n﹣4 , 设cn= ![]() ,若在数列{cn}中c6<cn(n∈N* , n≠6),则p的取值范围( )
,若在数列{cn}中c6<cn(n∈N* , n≠6),则p的取值范围( )
A.(11,25)
B.(12,22)
C.(12,17)
D.(14,20)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =![]() ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = ![]() ,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.
,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF.

(1)若以F、B、C、D为顶点的三棱锥的体积记为![]() ,求
,求![]() 的最大值;
的最大值;
(2)当 ![]() 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,曲线y=f(x)在点x=e2处的切线与直线x﹣2y+e=0平行.
,曲线y=f(x)在点x=e2处的切线与直线x﹣2y+e=0平行.
(1)若函数g(x)= ![]() f(x)﹣ax在(1,+∞)上是减函数,求实数a的最小值;
f(x)﹣ax在(1,+∞)上是减函数,求实数a的最小值;
(2)若函数F(x)=f(x)﹣ ![]() 无零点,求k的取值范围.
无零点,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2014 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com