
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|; ?
(3)设函数g(x)=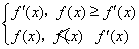 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
(1)a≥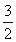 (2) x=1或x=-(1+2a) (3)4a+5
(2) x=1或x=-(1+2a) (3)4a+5
【解析】(1)因为f(x)≤f′(x),所以x2-2x+1≤2a(1-x),
又因为-2≤x≤-1, ?
所以a≥ max在x∈[-2,-1]时恒成立,因为
max在x∈[-2,-1]时恒成立,因为 =
= ≤
≤ ,
,
所以a≥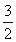 .(4分)
.(4分)
(2)因为f(x)=|f′(x)|,所以x2+2ax+1=2|x+a|,
所以(x+a)2-2|x+a|+1-a2=0,则|x+a|=1+a或|x+a|=1-a.(7分)
①当a<-1时,|x+a|=1-a,所以x=-1或x=1-2a;
②当-1≤a≤1时,|x+a|=1-a或|x+a|=1+a,
所以x=±1或x=1-2a或x=-(1+2a);
③当a>1时,|x+a|=1+a,所以x=1或x=-(1+2a).(10分)
(3)因为f(x)-f′(x)=(x-1)[x-(1-2a)],g(x)=
①若a≥- ,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
,则x∈[2,4]时,f(x)≥f′(x),所以g(x)=f′(x)=2x+2a,
从而g(x)的最小值为g(2)=2a+4;(12分)
②若a<-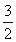 ,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
,则x∈[2,4]时,f(x)<f′(x),所以g(x)=f(x)=x2+2ax+1,
当-2≤a<-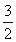 时,g(x)的最小值为g(2)=4a+5,
时,g(x)的最小值为g(2)=4a+5,
当-4<a<-2时,g(x)的最小值为g(-a)=1-a2,
当a≤-4时,g(x)的最小值为g(4)=8a+17.(14分)
③若-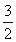 ≤a<-
≤a<- ,则x∈[2,4]时,
,则x∈[2,4]时,
g(x)=
当x∈[2,1-2a)时,g(x)最小值为g(2)=4a+5;
当x∈[1-2a,4]时,g(x)最小值为g(1-2a)=2-2a.
因为-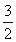 ≤a<-
≤a<- ,(4a+5)-(2-2a)=6a+3<0,
,(4a+5)-(2-2a)=6a+3<0,
所以g(x)最小值为4a+5,
综上所述,
[g(x)]min= (16分)
(16分)


科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
A.a100=-1,S100=5 B.a100=-3,S100=5
C.a100=-3,S100=2 D.a100=-1,S100=2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:填空题
函数g(x)=x2-2 013x,若g(a)=g(b),a≠b,则g(a+b)=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-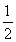 ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练B组练习卷(解析版) 题型:解答题
已知函数f(x)=-x3+x2,g(x)=aln x,a∈R.
(1)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求a的取值范围;
(2)设F(x)= 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,且c=2,C=60°.
(1)求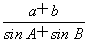 的值;
的值;
(2)若a+b=ab,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A,B两点,则弦AB的长等于________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练E组练习卷(解析版) 题型:填空题
图1是某学生的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14.图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是________.
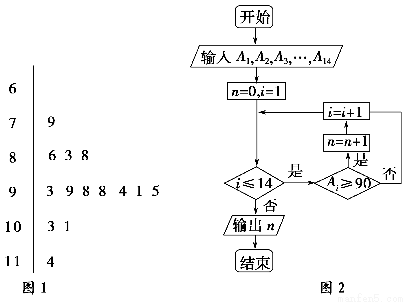
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练B组练习卷(解析版) 题型:填空题
若实数x,y满足 ,则x2+(y+1)2的最大值与最小值的差为________.
,则x2+(y+1)2的最大值与最小值的差为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com