
【题目】证明.
(1)用数学归纳法证明:12+22+32+…+n2= ![]() ,n是正整数;
,n是正整数;
(2)用数学归纳法证明不等式:1+ ![]() +
+ ![]() +…+
+…+ ![]() <2
<2 ![]() (n∈N*)
(n∈N*)
【答案】
(1)证明:①n=1时,左边=12=1,右边= ![]() =1,等式成立,
=1,等式成立,
②假设n=k时,等式成立,即12+22+32+…+k2= ![]() ,
,
则n=k+1时,12+22+32+…+k2+(k+1)2= ![]() +(k+1)2
+(k+1)2
= ![]() [2k2+k+6(k+1)]
[2k2+k+6(k+1)]
= ![]() (2k2+7k+6)
(2k2+7k+6)
= ![]() =
= ![]() .
.
∴当n=k+1时,等式成立,
由①②得:12+22+32+…+n2= ![]() .
.
(2)证明:①n=1时,显然不等式成立,
②假设n=k时,不等式成立,即1+ ![]() +
+ ![]() +…+
+…+ ![]() <2
<2 ![]() .
.
则当n=k+1时,1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() <2
<2 ![]() +
+ ![]() =
= ![]() <
< ![]() =2
=2 ![]() .
.
∴当n=k+1时,不等式成立.
由①②得1+ ![]() +
+ ![]() +…+
+…+ ![]() <2
<2 ![]() .
.
【解析】根据数学归纳法的证明步骤先验证n=1时结论成立,再假设n=k时,结论成立,推导n=k+1时结论成立即可.
【考点精析】认真审题,首先需要了解数学归纳法的定义(数学归纳法是证明关于正整数n的命题的一种方法).


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(2)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(3)记ξ表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数m取什么数值时,复数z=m2﹣1+(m2﹣m﹣2)i分别是:
(1)实数?
(2)虚数?
(3)纯虚数?
(4)表示复数z的点在复平面的第四象限?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ,sin25°+sin265°+sin2125°=
,sin25°+sin265°+sin2125°= ![]() .通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
.通过观察上述两等式的规律,请你写出一般性的命题,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 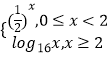 ,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)﹣a﹣1=0(a∈R)有且只有7个不同实数根,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M(x,y)在|x|≤1,|y|≤1时按均匀分布出现,试求满足:
(1)x+y≥0的概率;
(2)x+y<1的概率;
(3)x2+y2≥1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com