【题目】为了得到函数
的图象，只需把函数
，
的图象上所有的点（ ）
A.向左平移
个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）
B.向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）
C.向左平移个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）
D.向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍（纵坐标不变）
【答案】C
【解析】
按照平移变换和周期变换的结论，分别求出四个选项中得到的函数解析式可得答案.
对于
，把函数
，
的图象上所有的点向左平移
个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）得到函数
的图象，故不正确；
对于
，把函数，的图象上所有的点向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍（纵坐标不变）得到函数
的图象，故不正确；
对于
，把函数，的图象上所有的点向左平移个单位长度，再把所得各点的横坐标伸长到原来的
倍（纵坐标不变）得到函数
的图象，故正确；
对于
，把函数，的图象上所有的点向右平移个单位长度，再把所得各点的横坐标伸长到原来的倍（纵坐标不变）得到函数
的图象，故不正确.
故选：C.
科目：高中数学 来源： 题型：
【题目】在“数学发展史”知识测验后,甲、乙、丙三人对成绩进行预测:
甲说:我的成绩比乙高;
乙说:丙的成绩比我和甲的都高;
丙说:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人中预测正确的是________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点分别为
，过点
的直线与椭圆
交于
两点，
的周长为8，直线
被椭圆截得的线段长为
.
（1）求椭圆的方程；
（2）设
是椭圆上两动点，线段
的中点为
，
的斜率分别为
（
为坐标原点），且
，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的左、右焦点分别为
，
，椭圆的长轴长与焦距之比为
，过
的直线
与交于
，
两点.
（1）当的斜率为
时，求
的面积；
（2）当线段
的垂直平分线在
轴上的截距最小时，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出以下五个结论：
①函数
是偶函数；
②当
时，函数
的值域是
；
③等差数列
的前
项和为
，若
，则
；
④已知定义域为
的函数
，当且仅当
时，
成立.
函数
的最小值4；
则上述结论中正确的是______（写出所有正确结论的序号）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（2）（本小题满分7分）选修4-4：坐标系与参数方程
在直接坐标系
中，直线l的方程为x-y+4=0，曲线C的参数方程为
.
（I）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
（II）设点Q是曲线C上的一个动点，求它到直线l的距离的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC﹣A1B1C1中，E，F分别为A1C1和BC的中点，M，N分别为A1B和A1C的中点.求证：
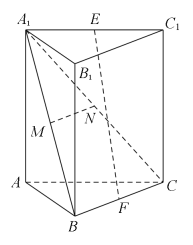
（1）MN∥平面ABC；
（2）EF∥平面AA1B1B.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为抑制房价过快上涨和过度炒作，各地政府响应中央号召，因地制宜出台了系列房价调控政策．某市为拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度，对年龄在
岁的人群中随机调查100人，调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如下：
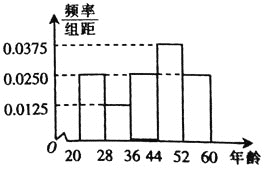
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
（1）由以上统计数据填
列联表，并判断能否在犯错误的概率不超过
的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异；
44岁以下 | 44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
（2）若以44岁为分界点，从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会．现从这8人中随机抽2人．
①抽到1人是44岁以下时，求抽到的另一人是44岁以上的概率．
②记抽到44岁以上的人数为X，求随机变量X的分布列及数学期望．
参考数据：
|
|
|
|
|
|
|
|
|
|
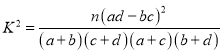，其中
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
