
| A. | 2 | B. | -2 | ||
| C. | |$\overrightarrow{AB}$|cosA | D. | 与菱形的边长有关 |
分析 设对角线AC与BD交与点O,易得AC、BD互相垂直且平分,再根据$\overrightarrow{CA}$•$\overrightarrow{AB}$=-|$\overrightarrow{AC}$|•|$\overrightarrow{AB}$|•cos∠BAC=-|$\overrightarrow{AC}$|×|$\overrightarrow{AO}$|,从而得出结论.
解答 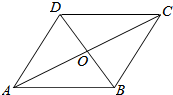 解:如图:菱形ABCD中,若AC=2,对角线AC与BD交与点O,易得AC、BD互相垂直且平分,
解:如图:菱形ABCD中,若AC=2,对角线AC与BD交与点O,易得AC、BD互相垂直且平分,
则$\overrightarrow{CA}$•$\overrightarrow{AB}$=-$\overrightarrow{AC}$•$\overrightarrow{AB}$=-|$\overrightarrow{AC}$|•|$\overrightarrow{AB}$|•cos∠BAC=-2×|$\overrightarrow{AO}$|=-2×1=-2,
故选:B.
点评 本题考查向量数量积的概念与计算,注意结合菱形的对角线的性质,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | x轴对称 | B. | 原点对称 | C. | y轴对称 | D. | 直线x=$\frac{π}{2}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
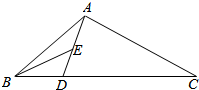 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
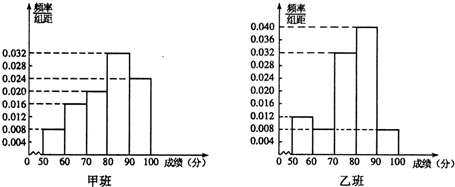
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com