
����Ŀ��ij�������ϰ�߷�ʱ�ζԼס�����������վ�������ȡ��50���˿ͣ�ͳ����˳��ȴ�ʱ�䣨ָ�˿ʹӽ�վ�ڵ����ϳ���ʱ�䣬��λ�����ӣ���ͳ�����ݰ�![]() ��
��![]() ��
��![]() ������
������![]() ���飬�Ƴ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
���飬�Ƴ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
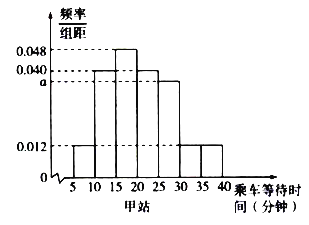
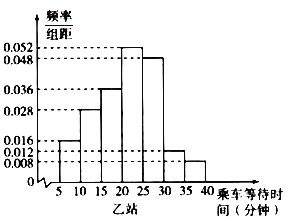
��1����a��ֵ��
��2����A��ʾ�¼������ϰ�߷�ʱ��ij�˿��ڼ�վ�˳��ȴ�ʱ������20���ӡ��Թ���A�ĸ��ʣ�
��3������ͬ���е�ÿ�������ø���������˵�ֵ�����ƣ������ϰ�߷�ʱ�μס�����վ����ȡ��50���˿ͳ˳���ƽ���ȴ�ʱ��ֱ�Ϊ![]() ����
����![]() ��ֵ����ֱ��д��
��ֵ����ֱ��д��![]() ��
��![]() �Ĵ�С��ϵ.
�Ĵ�С��ϵ.
���𰸡���1��![]() ��2��0.5��3��
��2��0.5��3��![]()
![]() ��
��![]()
��������
��1������С�����ε������Ϊ![]() �з��̣��ⷽ�����
�з��̣��ⷽ�����![]() ��ֵ.
��ֵ.
��2������Ƶ�ʷֲ�ֱ��ͼ��������˿��ڼ�վ�ȴ�ʱ������20���ӵ�Ƶ�ʣ��ɴ˹���A�ĸ���.
��3������Ƶ�ʷֲ�ֱ��ͼ�����ƽ����![]() .����ͼ���жϳ�
.����ͼ���жϳ�![]() .
.
��1����Ϊ![]() ��
��
����![]() .
.
��2��������֪���ó˿��ڼ�վ�ȴ�ʱ������20���ӵ�Ƶ��Ϊ![]() ����
����![]() �Ĺ���ֵΪ0.5.
�Ĺ���ֵΪ0.5.
��3��![]()
![]() .
.
��ֱ��ͼ֪![]() .����Ϊ��ͼ�нϸߵ�С������λ�ڵȴ�ʱ��ϳ��ķ�Χ��
.����Ϊ��ͼ�нϸߵ�С������λ�ڵȴ�ʱ��ϳ��ķ�Χ��


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��50��ѧ�����п�����ѧ�ɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ,���гɼ�����������:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].�������ɼ�������80�ֵ�ѧ�������ѡȡ2��,����2�˳ɼ���90������(��90��)������Ϊ��,��ε���ѧ����Ϊ( )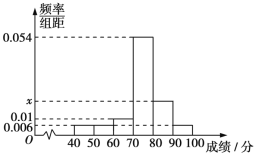
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ���ı���
���ı���![]() �����Σ���
�����Σ���![]() ���߶�
���߶�![]() ��.
��.
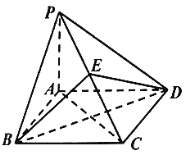
��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() �������
�������![]() ������ֵΪ
������ֵΪ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㾭�����ҹ����ϵ�����ѧ����ѧ�����������м��أ�һ���ж�ʮ�ĸ�������ÿ�������г�������ͬ�����ǰ�����Ӱ�ⶨʱ�̵��������г���Ϊ����Ӱ�ӵij��ȣ���������С������������¶����֡���¶��˪���������ľŸ����������г����γɵȲ����У�����¼���㣬��Ÿ������������г�֮��Ϊ49.5�ߣ�����������������������г�֮��Ϊ10.5�ߣ���������г�Ϊ�� ��
A.1.5��B.2.5��C.3.5��D.4.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������eΪ��Ȼ�����ĵ���.
������eΪ��Ȼ�����ĵ���.
��1��������![]() �ļ�СֵΪ
�ļ�СֵΪ![]() ����
����![]() ��ֵ��
��ֵ��
��2����![]() ��֤������
��֤������![]() ʱ��
ʱ��![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1������![]() ��
��![]() ����������ͬ���
����������ͬ���![]()
![]()
![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2���ڵڣ�1���ʵ��������жϵ�![]() ʱ������
ʱ������![]() �Ƿ�λ��
�Ƿ�λ��![]() ���·�����˵�����ɣ�
���·�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y2=4x�Ľ����ֱ��l�������߽���A��B���㣬���M��3��0��.����MAB�����Ϊ![]() ����|AB|=( )
����|AB|=( )
A.2B.4C.![]() D.8
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����C��![]() 1��a��0��b��0���Ľ���ֱ�ΪF1����5��0����F2��5��0����PΪC��һ�㣬PF1��PF2��tan��PF1F2
1��a��0��b��0���Ľ���ֱ�ΪF1����5��0����F2��5��0����PΪC��һ�㣬PF1��PF2��tan��PF1F2![]() ����C�ķ���Ϊ�� ��
����C�ķ���Ϊ�� ��
A.x2![]() 1B.
1B.![]() y2��1
y2��1
C.![]() 1D.
1D.![]() 1
1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ϊ�˹�����У��ҵ��������ҵ����̨�������Ż����ߣ��Դ�ҵ������ҵ��ij��У��ҵ��С��������ҵ���º��ʵ��������ۣ���ÿ����ÿ��300Ԫ�ļ۸����ΧϺ��Ȼ����ÿ��500Ԫ�ļ۸���ۣ�������칺��Ļ�ΧϺ�����꣬ʣ��ľ�������������Ϊ�˶��Լ��ľ�Ӫ״���и������İ��գ�����¼��150���ΧϺ��������������λ���䣩���Ƴ���ͼ��ʾ��Ƶ���ֲ�����ͼ��

��1����С��һ�칺��12���ΧϺ��
�����������![]() ����λ��Ԫ�����ڵ����������
����λ��Ԫ�����ڵ����������![]() ����λ���䣬
����λ���䣬![]() ���ĺ�������ʽ��
���ĺ�������ʽ��
������150���¼������������Ƶ����Ϊ���ʣ������������1900Ԫ�ĸ��ʣ�
��2������������������Ϊ���ߵ����ݣ����ƻ����ÿ�칺����ΧϺ��������ͬ�����ڽ�����Ϊ11�䣬12����ѡ����һ������ȷ�������ķ�������ʹ���������ƽ���������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com