
【题目】已知函数f(x)=lnx﹣ax2﹣bx(a,b∈R),g(x)= ![]() ﹣lnx.
﹣lnx.
(1)当a=﹣1时,f(x)与g(x)在定义域上的单调性相反,求b的取值范围;
(2)当a,b都为0时,斜率为k的直线与曲线y=f(x)交A(x1 , y1),B(x2 , y2)(x1<x2)于两点,求证:x1< ![]() .
.
【答案】
(1)解:∵a=﹣1∴f(x)=lnx+x2﹣bx,由题意可知,f(x)与g(x)的定义域都为(0,+∞).
∵  =
= 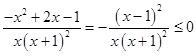
∴g(x)在(0,+∞)上单调递减.
又a=﹣1时,f(x)与g(x)在定义域上的单调性相反,
∴f(x)=lnx+x2﹣bx在(0,+∞)上单调递增.
∴ ![]() 对x∈(0,+∞)恒成立
对x∈(0,+∞)恒成立
即 ![]() 对x∈(0,+∞)恒成立,∴只需
对x∈(0,+∞)恒成立,∴只需 ![]() ,
,
∵x>0,∴ ![]() (当且仅当
(当且仅当 ![]() 时,等号成立),
时,等号成立),
∴ ![]() ,∴b的取值范围为
,∴b的取值范围为 ![]() .
.
(2)证明: ![]() .
.
要证 ![]() ,即证
,即证 ![]() ,
,
等价于证 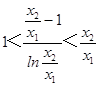 ,令
,令 ![]() ,
,
则只要证 ![]() ,由t>1,知lnt>0,
,由t>1,知lnt>0,
故等价于证lnt<t﹣1<tlnt(t>1),(*)
设m(t)=t﹣1﹣lnt(t>1),则 ![]() ,
,
故m(t)在(1,+∞)上是增函数,
当t>1时,m(t)=t﹣1﹣lnt>m(1)=0,即t﹣1>lnt.
设h(t)=tlnt﹣(t﹣1)(t>1),则h'(t)=lnt>0(t>1),
故h(t)在(1,+∞)上是增函数.
当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1<tlnt(t>1).
由可知(*)成立,故 ![]()
【解析】(1)化简函数f(x)=lnx+x2﹣bx,求出f(x)与g(x)的定义域都为(0,+∞).求出函数的导数,判断g(x)在(0,+∞)上单调递减,利用f(x)与g(x)在定义域上的单调性相反,推出 ![]() 对x∈(0,+∞)恒成立,即
对x∈(0,+∞)恒成立,即 ![]() 对x∈(0,+∞)恒成立利用基本不等式求解最值,即可.(2)
对x∈(0,+∞)恒成立利用基本不等式求解最值,即可.(2) ![]() .要证
.要证 ![]() ,等价于证
,等价于证 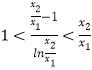 ,令
,令 ![]() ,等价于证lnt<t﹣1<tlnt(t>1),设m(t)=t﹣1﹣lnt(t>1),则
,等价于证lnt<t﹣1<tlnt(t>1),设m(t)=t﹣1﹣lnt(t>1),则 ![]() ,通过函数的单调性转化求解即可.
,通过函数的单调性转化求解即可.
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若焦点在x轴上的椭圆C的焦距为2,且离心率为 ![]() .
.
(1)求椭圆C的标准方程;
(2)若经过点(0, ![]() )且斜率为k的直线l与椭圆C有两个不同的交点P和Q. (Ⅰ)求k的取值范围;
)且斜率为k的直线l与椭圆C有两个不同的交点P和Q. (Ⅰ)求k的取值范围;
(Ⅱ)设椭圆C与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量 ![]() 与
与 ![]() 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0),A1 , A2是实轴顶点,F是右焦点,B(0,b)是虚轴端点,若在线段BF上(不含端点)存在不同的两点p1(i=1,2),使得△PiA1A2(i=1,2)构成以A1A2为斜边的直角三角形,则双曲线离心率e的取值范围是( )
=1(a>0,b>0),A1 , A2是实轴顶点,F是右焦点,B(0,b)是虚轴端点,若在线段BF上(不含端点)存在不同的两点p1(i=1,2),使得△PiA1A2(i=1,2)构成以A1A2为斜边的直角三角形,则双曲线离心率e的取值范围是( )
A.( ![]() ,+∞)
,+∞)
B.( ![]() ,+∞)
,+∞)
C.(1, ![]() )
)
D.( ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,已知角A,B,C所对的边分别为a,b,c, ![]() +
+ ![]() =
= ![]() ,b=4,且a>c.
,b=4,且a>c.
(1)求ac的值;
(2)若△ABC的面积为2 ![]() ,求a,c的值.
,求a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2 , |F1F2|=4,P是双曲线右支上的一点,F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=1,则双曲线的离心率是( ) 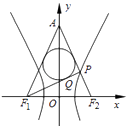
A.3
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设函数 ![]() ,若在[1,e]上至少存在一点x0 , 使得f(x0)≥g(x0)成立,求实数a的取值范围.
,若在[1,e]上至少存在一点x0 , 使得f(x0)≥g(x0)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2017年初的时候,国家政府工作报告明确提出,2017年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,6月至11月的用煤量如下表所示:

(1)由于某些原因, ![]() 中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
中一个数据丢失,但根据6至9月份的数据得出少样本平均值是3.5,求出丢失的数据;
(2)请根据6至9月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与10月11月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过0.3,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?(参考公式:线性回归方程![]() ,其中
,其中 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com