
分析 根据同角的三角函数的关系和两角差的正弦公式即可求出.
解答 解:∵0<α<$\frac{π}{2}$,
∴$\frac{π}{6}$$<α+\frac{π}{6}$<$\frac{2π}{3}$,
∵$cos(α+\frac{π}{6})=\frac{3}{5}$,
∴sin($α+\frac{π}{6}$)=$\frac{4}{5}$,
∵$sin(α-\frac{π}{6})$=sin(α+$\frac{π}{6}$-$\frac{π}{3}$)=sin(α+$\frac{π}{6}$)cos$\frac{π}{3}$-cos(α+$\frac{π}{6}$)sin$\frac{π}{3}$=$\frac{4}{5}$×$\frac{1}{2}$-$\frac{3}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$,
故答案为:$\frac{4-3\sqrt{3}}{10}$
点评 本题考查了同角的三角函数的关系和两角差的正弦公式,属于基础题.


科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:解答题
甲、乙两人玩一种游戏:在装有质地、大小完全相同,编号分别为1,2,3,4,5,6的6个球的口袋中,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数则甲赢,否则乙赢.
(1)求甲赢且编号和为8的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 自2008年起,每年的生活垃圾无害化处理量和年份代码正相关 | |
| B. | 自2008年起,每年的生活垃圾无害化处理量大约增加0.10万吨 | |
| C. | 由此模型可知2016年该地区生活垃圾无害化处理量是1.82万吨 | |
| D. | 由此模型预测出2017年该地区生活垃圾无害化处理量约为1.92万吨 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
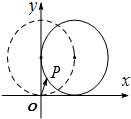 如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )
如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(1,1)时,$\overrightarrow{OP}$的坐标为( )| A. | (1-sin1,1-cos1) | B. | (1+sin1,1-cos1) | C. | (1-sin1,1+cos1) | D. | (1+sin1,1+cos1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com