
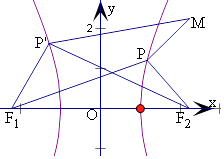
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4 ![]() ,P(x,y)在双曲线上,M(
,P(x,y)在双曲线上,M( ![]() ,
, ![]() ),则|PM|+|PF2|的最小值为( )
),则|PM|+|PF2|的最小值为( )
A.![]() ﹣1
﹣1
B.2
C.2 ![]() ﹣2
﹣2
D.3
【答案】D
【解析】解:双曲线的左、右焦点分别为F1(﹣c,0),F2(c,0),
渐近线方程为y=± ![]() x,
x,
令x=c,解得y=± ![]() ,
,
可得|AB|= ![]() ,
,
若△ABF1为等腰直角三角形,且|AB|=4 ![]() ,
,
即有 ![]() =4
=4 ![]() ,2c=2
,2c=2 ![]() ,c2=a2+b2,
,c2=a2+b2,
解得a=1,b=2,c= ![]() ,
,
即有双曲线的方程为x2﹣ ![]() =1,
=1,
由题意可知若P在左支上,由双曲线的定义可得|PF2|=2a+|PF1|,
|PM|+|PF2|=|PM|+|PF1|+2a≥|MF1|+2= ![]() +2=7,
+2=7,
当且仅当M,P,F1共线时,取得最小值7;
若P在右支上,由双曲线的定义可得|PF2|=|PF1|﹣2a,
|PM|+|PF2|=|PM|+|PF1|﹣2a≥|MF1|﹣2= ![]() ﹣2=3,
﹣2=3,
当且仅当M,P,F1共线时,取得最小值3.
综上可得,所求最小值为3.
故选:D.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为 ![]() . (Ⅰ)求选手甲可进入决赛的概率;
. (Ⅰ)求选手甲可进入决赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平行四边形ABCD中,A(1,2),B(2,1),中心E(3,3).
(1)判断平行四边形ABCD是否为正方形;
(2)点P(x,y)在平行四边形ABCD的边界及内部运动,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0),直线l与抛物线C相交于A,B两点,P为抛物线上一点,当直线l过抛物线焦点时,|AB|的最小值为2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若AB的中点为(3,1),且直线PA,PB的倾斜角互补,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com