
【题目】已知x,y,z均为正数.
(1)若xy<1,证明:|x+z||y+z|>4xyz;
(2)若![]() =
=![]() ,求2xy2yz2xz的最小值.
,求2xy2yz2xz的最小值.
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,四边形ACFE为平行四边形,设BD与AC相交于点G,AB=BD=AE=2,∠EAD=∠EAB.

(1)证明:平面ACFE⊥平面ABCD;
(2)若直线AE与BC的夹角为60°,求直线EF与平面BED所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了庆祝中华人民共和国成立70周年,某公司举行大型抽奖活动,活动中准备了一枚质地均匀的正十二面体的骰子,在其十二个面上分别标有数字1,2,3,…,12,每位员工均有一次参与机会,并规定:若第一次抛得向上面的点数为完全平方数(即能写成整数的平方形式,如![]() ),则立即视为获得大奖;若第一次抛得向上面的点数不是完全平方数,则需进行第二次抛掷,两次抛得的点数和为完全平方数(如
),则立即视为获得大奖;若第一次抛得向上面的点数不是完全平方数,则需进行第二次抛掷,两次抛得的点数和为完全平方数(如![]() ),也可视为获得大奖.否则,只能获得安慰奖.
),也可视为获得大奖.否则,只能获得安慰奖.
(1)试列举须抛掷两次才能获得大奖的所有可能情况(用![]() 表示前后两次抛得的点数),并说明所有可能情况的总数;
表示前后两次抛得的点数),并说明所有可能情况的总数;
(2)若获得大奖的奖金(单位:元)为抛得的点数或点数和(完全平方数)的360倍,而安慰奖的奖金为48元,该公司某位员工获得的奖金为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,AC=![]() BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
BC,AB=2BC,D为线段AB上一点,且AD=3DB,PD⊥平面ABC,PA与平面ABC所成的角为45°.
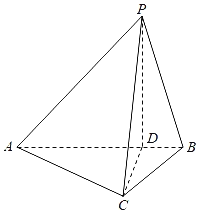
(1)求证:平面PAB⊥平面PCD;
(2)求二面角P﹣AC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我们的教材必修一中有这样一个问题,假设你有一笔资金,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报![]() 元;
元;
方案二:第一天回报![]() 元,以后每天比前一天多回报
元,以后每天比前一天多回报![]() 元;
元;
方案三:第一天回报![]() 元,以后每天的回报比前一天翻一番.
元,以后每天的回报比前一天翻一番.
记三种方案第![]() 天的回报分别为
天的回报分别为![]() ,
,![]() ,
,![]() .
.
(1)根据数列的定义判断数列![]() ,
,![]() ,
,![]() 的类型,并据此写出三个数列的通项公式;
的类型,并据此写出三个数列的通项公式;
(2)小王准备做一个为期十天的短期投资,他应该选择哪一种投资方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有下列四个结论,其中所有正确结论的编号是___________.
①若![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
②若![]() ,
,![]() ,
,![]() 是等差数列
是等差数列![]() 的前
的前![]() 项,则
项,则![]() ;
;
③“![]() ”的一个必要不充分条件是“
”的一个必要不充分条件是“![]() ”;
”;
④“![]() ,
,![]() ”的否定为“
”的否定为“![]() ,
,![]() ”.
”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com