【答案】
分析:(1)分别化简A和B两个集合,找出A=B 的等价条件,即得要证结论.
(2))“
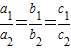
”是“A=B”的充分不必要条件,利用比例式的性质证明充分性成立,通过举反例可得必要性
不成立.
(3)通过给变量取特殊值,举反例可得充分性和必要性都不成立,从而得到“
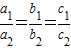
”是“A=B”的既不充分
也不必要条件.
解答:解:(1)因为
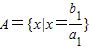
,
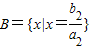
,故
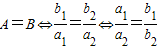
,
故命题成立.…..(4分)
(2)“
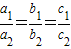
”是“A=B”的充分不必要条件. …..(6分)
证明:充分性:
若x
∈A,即x
是方程a
1x
2+b
1x+c
1=0的解,则a
1x
2+b
1x
+c
1=0,
而非零实数a
1,b
1,c
1和a
2,b
2,c
2满足
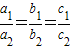
,
设

,则可得k(a
2x
2+b
2x
+c
2)=0,
所以a
2x
2+b
2x
+c
2=0,即x
是方程a
2x
2+b
2x+c
2=0的解,即x
∈B,
于是A⊆B.同理可证B⊆A,所以A=B. …..(10分)
必要性不成立,例如:当A=B=ϕ 时,不能推出
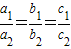
成立.…..(11分)
(3)如果系数a
1,b
1,c
1和a
2,b
2,c
2都是非零实数,不等式a
1x
2+b
1x+c
1>0和a
2x
2+b
2x+c
2>0的解集分别是A和B,
则“
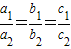
”是“A=B”的既不充分也不必要条件.
如 a
1 =1,b
1=2,c
1=-3,a
2=-2,b
2,=-4,c
2=6 时,
A={x|a
1x
2+b
1x+c
1>0,a
1b
1c
1≠0}={x|x
2+2x-3>0}={x|x<-3,或 x>1 },
B=x|a
2x
2+b
2x+c
2>0,a
2b
2c
2≠0}={x|-2x
2-4x+6>0}={x|x
2+2x-3<0}={x|-3<x<1},
显然,A≠B.故成分性不成立. …..(14分)
当A=B 时,a
1 =1,b
1=2,c
1=3,a
2=1,b
2,=-4,c
2=6 时,
A={x|x
2+2x+3>0}={x|x∈R}=R,B=x|x
2 -4x+6>0}={x|x∈R}=R,
显然不满足
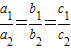
,故必要性也不成立. …..(16分)
点评:本题主要考查充分条件、必要条件、充要条件的定义,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法,体现了转化的数学思想,属于中档题.

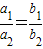 ;
;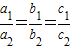 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程;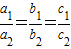 是A=B的什么条件?请给出说明过程.
是A=B的什么条件?请给出说明过程.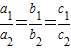 ”是“A=B”的充分不必要条件,利用比例式的性质证明充分性成立,通过举反例可得必要性
”是“A=B”的充分不必要条件,利用比例式的性质证明充分性成立,通过举反例可得必要性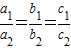 ”是“A=B”的既不充分
”是“A=B”的既不充分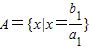 ,
,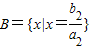 ,故
,故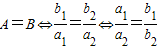 ,
,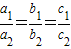 ”是“A=B”的充分不必要条件. …..(6分)
”是“A=B”的充分不必要条件. …..(6分)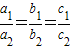 ,
, ,则可得k(a2x2+b2x+c2)=0,
,则可得k(a2x2+b2x+c2)=0,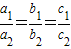 成立.…..(11分)
成立.…..(11分)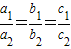 ”是“A=B”的既不充分也不必要条件.
”是“A=B”的既不充分也不必要条件. 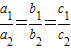 ,故必要性也不成立. …..(16分)
,故必要性也不成立. …..(16分)

 名校课堂系列答案
名校课堂系列答案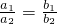 ;
;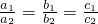 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程; ;
;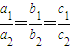 是A=B的什么条件?请给出说明过程;
是A=B的什么条件?请给出说明过程;