
| A. | ①② | B. | ③④ | C. | ①③ | D. | ①③④ |
分析 对于函数①y=x3,取任意的x1∈R,x2=$\root{3}{4-{{x}_{1}}^{3}}$,可以得到唯一的x2∈D满足条件;对于函数②y=4sinx,y=4sinx是R上的周期函数,存在无穷个的x2∈D,使$\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立;对于函数③y=lnx,定义域为x>0,值域为R且单调,存在唯一的x2∈D,使 $\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立;对于函数④y=2x,当x1=3,f(x1)=8.要使 $\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立,则f(x2)=-4,不成立.
解答 解:对于函数①y=x3,取任意的x1∈R,$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{{{x}_{1}}^{3}+{{x}_{2}}^{3}}{2}$=2,x2=$\root{3}{4-{{x}_{1}}^{3}}$,
可以得到唯一的x2∈D.满足条件,故①成立;
对于函数②y=4sinx,因为y=4sinx是R上的周期函数,
存在无穷个的x2∈D,使$\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立.不满足条件,故②不成立;
对于函数③y=lnx,定义域为x>0,值域为R且单调,
必存在唯一的x2∈D,使 $\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立.故③成立;
对于函数④y=2x定义域为R,值域为y>0.对于x1=3,f(x1)=8.
要使 $\frac{f({x}_{1})+f({x}_{2})}{2}$=2成立,则f(x2)=-4,不成立,故④不成立.
故选:C.
点评 本题考查均值为2的函数的判断,是基础题,解题时要认真审题,注意函数性质的合理运用.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条直线都和同一个平面平行,则这两条直线平行 | |
| B. | 两条直线没有公共点,则这两条直线平行 | |
| C. | 两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 一条直线和一个平面内所有直线没有公共点,则这条直线和这个平面平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .1条 | B. | .2条 | C. | .3条 | D. | .4条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
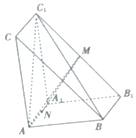 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{6}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com