
【题目】已知函数f(x)=ax2+8x+b(a,b为互不相等的正整数),方程f(x)=0的两个实根为x1 , x2(x1≠x2),且|x1|<1,|x2|<1,若f(1)+f(﹣1)的最大值与最小值分别为M,m,则M+m的值为 .
【答案】50
【解析】解:f(x)=ax2+8x+b,
此函数的图象与x轴的两个交点在区间(﹣1,1),
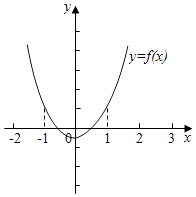
∴ 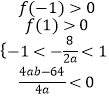
∴  即有
即有 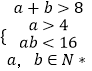 ,
,
∵a,b为互不相等的正整数,
∴a,b可能的取值有(7,2)(8,1)(9,1)(10,1),
(11,1),(12,1),(13,1),(14,1)(15,1)共9个.
∴a+b的最小值是9,最大值为16.
则f(1)+f(﹣1)=2(a+b)的最大值与最小值分别为M=32,m=18,
可得M+m=50.
故答案为:50.
由|x1|<1,|x2|<1知,方程的两根在区间(﹣1,1)内,f(x)=ax2+8x+b,此函数的图象与x轴的两个交点在区间(﹣1,1)内,可得,f(﹣1)>0,f(1)>0,且对称轴在区间(﹣1,1)内,最小值小于0.由此列条件求a+b的最值,进而得到M+m的和.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为正整数集的函数f(x)= 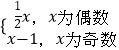 ,f1(x)=f(x),fn(x)=f[fn﹣1(x)].若fn(21)=1,则n=;若f4(x)=1,则x所有的值构成的集合为 .
,f1(x)=f(x),fn(x)=f[fn﹣1(x)].若fn(21)=1,则n=;若f4(x)=1,则x所有的值构成的集合为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,a2n=n﹣an , a2n+1=an+1(n∈N*),则a1+a2+a3+…+a40等于( )
A.222
B.223
C.224
D.225
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4
,其左右焦点分别为F1 , F2 , 过F1的直线交椭圆于A,B两点,且△ABF2的周长为4 ![]() .
. 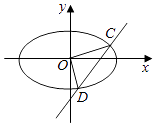
(1)求椭圆的方程;
(2)如图,直线x=ty+m交椭圆于不同两点C,D,若以线段CD为直径的圆过原点O,求|CD|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}分别满足a1=1,|an+1﹣an|=2,且 ![]() |=2,其中n∈N* , 设数列{an},{bn}的前n项和分别为Sn , Tn .
|=2,其中n∈N* , 设数列{an},{bn}的前n项和分别为Sn , Tn .
(1)若数列{an},{bn}都是递增数列,求数列{an},{bn}的通项公式;
(2)若数列{cn}满足:存在唯一的正整数k(k≥2),使得ck<ck﹣1 , 则称数列{cn}为“k坠点数列”. ①若数列{an}为“5坠点数列”,求Sn;
②若数列{an}为“p坠点数列”,数列{bn}为“q坠点数列”,是否存在正整数m使得Sm+1=Tm?若存在,求出m的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小学对五年级的学生进行体质测试,已测得五年级一班30名学生的跳远成绩(单位:cm),用茎叶图统计如图,男生成绩在175cm以上(包括175cm)定义为合格,成绩在175cm以下(不含175cm)定义为“不合格”;女生成绩在165以上(包括165cm)定义为“合格”,成绩在165cm以下(不含165cm)定义为“不合格”. 
(1)求男生跳远成绩的中位数.
(2)根据男女生的不同,用分层抽样的方法从该班学生中抽取1个容量为5的样本,求抽取的5人中女生的人数.
(3)以此作为样本,估计该校五年级学生体质的合格率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A.各个面都是三角形的几何体是三棱锥
B.一平面截一棱锥得到一个棱锥和一个棱台
C.棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥
D.圆锥的顶点与底面圆周上的任意一点的连线都是母线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com