
【题目】已知函数![]() ,
,![]() ,且
,且![]() 与
与![]() 的图象有一条斜率为1的公切线(e为自然对数的底数).
的图象有一条斜率为1的公切线(e为自然对数的底数).
(1)求![]() ;
;
(2)设函数![]() ,证明:当
,证明:当![]() 时,
时,![]() 有且仅有2个零点.
有且仅有2个零点.
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面BB1C1C为菱形,![]() .
.
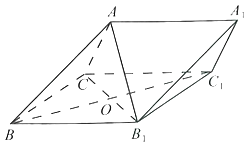
(1)求证:B1C⊥AB;
(2)若∠CBB1=60°,AC=BC,且点A在侧面BB1C1C上的投影为点O,求二面角B﹣AA1﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,P,Q,M,N,H,R是各条棱的中点.
中,P,Q,M,N,H,R是各条棱的中点.
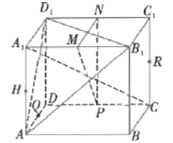
①直线![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四点共面;④
;③P,Q,H,R四点共面;④![]() 平面
平面![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年,新型冠状病毒来势凶猛,老百姓一时间“谈毒色变”,近来,有关喝白酒可以预防病毒的说法一直在民间流传,更有人拿出“医”字的繁体字“醫”进行解读为:医治瘟疫要喝酒,为了调查喝白酒是否有助于预防病毒,我们调查了1000人的喝酒生活习惯与最终是否得病进行了统计,表格如下:
每周喝酒量(两) |
|
|
|
|
|
人数 | 100 | 300 | 450 | 100 |
|
规定:①每周喝酒量达到4两的叫常喝酒人,反之叫不常喝酒人;
②每周喝酒量达到8两的叫有酒瘾的人.
(1)求![]() 值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
值,从每周喝酒量达到6两的人中按照分层抽样选出6人,再从这6人中选出2人,求这2人中无有酒瘾的人的概率;
(2)请通过上述表格中的统计数据,填写完下面的![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
列联表,并通过计算判断是否能在犯错误的概率不超过0.1的前提下认为是否得病与是否常喝酒有关?并对民间流传的说法做出你的判断.
常喝酒 | 不常喝酒 | 合计 | |
得病 | |||
不得病 | 250 | 650 | |
合计 |
参考公式: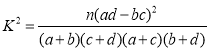 ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 和
和![]() 都是定义在
都是定义在![]() 上的单调减函数,且
上的单调减函数,且![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,
,![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 在
在![]() 上的“被追逐函数”,若
上的“被追逐函数”,若![]() ,下述四个结论中正确的是( )
,下述四个结论中正确的是( )
①![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
②若![]() 和函数
和函数![]() 关于
关于![]() 轴对称,则
轴对称,则![]() 是
是![]() 在
在![]() 上的“被追逐函数”;
上的“被追逐函数”;
③若![]() 是
是![]() 在
在![]() 上的“被追逐函数”,则
上的“被追逐函数”,则![]() ;
;
④存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“被追逐函数”.
上的“被追逐函数”.
A.①③④B.①②④C.②③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
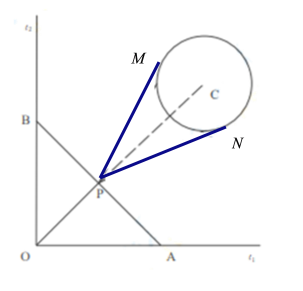
【题目】如图,在一旅游区内原有两条互相垂直且相交于点O的道路l1,l2,一自然景观的边界近似为圆形,其半径约为1千米,景观的中心C到l1,l2的距离相等,点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观,具体方案:在线段OC上取一点P,新建一条道路OP,并过点P新建两条与圆C相切的道路PM,PN(M,N为切点),同时过点P新建一条与OP垂直的道路AB(A,B分别在l1,l2上).为促进沿途旅游经济,新建道路长度之和越大越好,求新建道路长度之和的最大值.(所有道路宽度忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com