
【题目】已知函数![]() 相邻两个最高点的距离等于
相邻两个最高点的距离等于![]() .
.
(1)求![]() 的值;
的值;
(2)求出函数![]() 的对称轴,对称中心;
的对称轴,对称中心;
(3)把函数![]() 图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),得到函数
图象上所有点的纵坐标伸长到原来的3倍(横坐标不变),得到函数![]() ,再把函数
,再把函数![]() 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() ,不需要过程,直接写出函数
,不需要过程,直接写出函数![]() 的函数关系式.
的函数关系式.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲地,随着人们生活水平的不断提高,进入电影院看电影逐渐成为老百姓的一种娱乐方式.我们把习惯进入电影院看电影的人简称为“有习惯”的人,否则称为“无习惯的人”.某电影院在甲地随机调查了100位年龄在15岁到75岁的市民,他们的年龄的频数分布和“有习惯”的人数如下表:

(1)以年龄45岁为分界点,请根据100个样本数据完成下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“有习惯”的人与年龄有关;
的把握认为“有习惯”的人与年龄有关;

(2)已知甲地从15岁到75岁的市民大约有11万人,以频率估计概率,若每张电影票定价为![]() 元
元![]() ,则在“有习惯”的人中约有
,则在“有习惯”的人中约有![]() 的人会买票看电影(
的人会买票看电影(![]() 为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
为常数).已知票价定为30元的某电影,票房达到了 69.3万元.某新影片要上映,电影院若将电影票定价为25元,那么该影片票房估计能达到多少万元?
参考公式:![]() ,其中
,其中![]() .
.
参考临界值

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨![]() 年提出了一个著名的猜想:任给一个正整数
年提出了一个著名的猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半(即
是偶数,就将它减半(即![]() );如果
);如果![]() 是奇数,则将它乘
是奇数,则将它乘![]() 加
加![]() (即
(即![]() ),不断重复这样的运算,经过有限步后,一定可以得到
),不断重复这样的运算,经过有限步后,一定可以得到![]() .对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数
.对于科拉茨猜想,目前谁也不能证明,也不能否定.现在请你研究:如果对正整数![]() (首项)按照上述规则施行变换后的第
(首项)按照上述规则施行变换后的第![]() 项为
项为![]() (注:
(注:![]() 可以多次出现),则
可以多次出现),则![]() 的所有不同值的个数为( )
的所有不同值的个数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
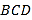
(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 且
且![]() .
.
(1)若函数![]() 是奇函数,试证明:对任意的
是奇函数,试证明:对任意的![]() ,恒有
,恒有![]() ;
;
(2)若对于![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值是3,试求实数
上的最大值是3,试求实数![]() 的值;
的值;
(3)设![]() 且
且![]() ,问:是否存在实数
,问:是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() ?如果存在,请求出
?如果存在,请求出![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com