
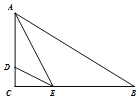
【题目】如图,在Rt△ABC中,![]() ,
,![]() ,AC=4,D在AC上且AD:DC=3:1,当∠AED最大时,△AED的面积为( )
,AC=4,D在AC上且AD:DC=3:1,当∠AED最大时,△AED的面积为( )
A.![]() B.2C.3D.
B.2C.3D.![]()
【答案】C
【解析】
根据条件得到![]() ,然后设∠AED=θ,∠AEC=α,∠DEC=β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当∠AED最大时,△AED的面积.
,然后设∠AED=θ,∠AEC=α,∠DEC=β,用两角差的正切公式求出tanθ,再用基本不等式求出tanθ最大值,从而得到当∠AED最大时,△AED的面积.
解:因为AD:DC=3:1,所以DC![]() AC=1,
AC=1,
所以S△AED=S△ACE﹣S△DEC![]() ACCE
ACCE![]() DCEC
DCEC
![]() ACCE
ACCE![]()
![]() ACCE=ACCE(
ACCE=ACCE(![]() ACEC.
ACEC.
因为AC=4,CE≤CB,而在Rt△ABC中,![]() ,AC=4,
,AC=4,
所以CB=4![]() ,∠AED=∠AEC﹣∠DEC.
,∠AED=∠AEC﹣∠DEC.
设∠AED=θ,∠AEC=α,∠DEC=β,
则tanθ=tan(α﹣β)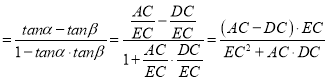
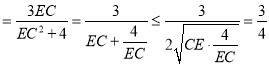 ,
,
当且仅当EC![]() ,即EC=2时,取等号,
,即EC=2时,取等号,
所以tanθ的最大值为![]() ,此时∠AED最大,
,此时∠AED最大,
所以当∠AED最大时,△AED的面积![]() =
=![]() 42=3.
42=3.
故选:C.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,在线段
,在线段![]() 上任取两点(端点A,B除外 ),将线段
上任取两点(端点A,B除外 ),将线段![]() 分成了三条线段,若分成的三条线段长度均为正整数,则这三条线段可以构成三角形的概率是 ____________;若分成的三条线段的长度均为正实数,则这三条线段可以构成三角形的概率是 _________.
分成了三条线段,若分成的三条线段长度均为正整数,则这三条线段可以构成三角形的概率是 ____________;若分成的三条线段的长度均为正实数,则这三条线段可以构成三角形的概率是 _________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店销售某海鲜,统计了春节前后50天该海鲜的需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为
,单位:公斤),其频率分布直方图如图所示,该海鲜每天进货1次,商店每销售1公斤可获利50元;若供大于求,剩余的削价处理,每处理1公斤亏损10元;若供不应求,可从其它商店调拨,销售1公斤可获利30元.假设商店每天该海鲜的进货量为14公斤,商店的日利润为![]() 元.
元.

(1)求商店日利润![]() 关于需求量
关于需求量![]() 的函数表达式;
的函数表达式;
(2)假设同组中的每个数据用该组区间的中点值代替.
①求这50天商店销售该海鲜日利润的平均数;
②估计日利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的半焦距为
的半焦距为![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 有且仅有两个公共点,直线
有且仅有两个公共点,直线![]() 与椭圆
与椭圆![]() 只有一个公共点.
只有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点,试问:
两点,试问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出该定值和点
为定值?若存在,求出该定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若命题甲是命题乙的充分非必要条件,命题丙是命题乙的必要非充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( )
A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
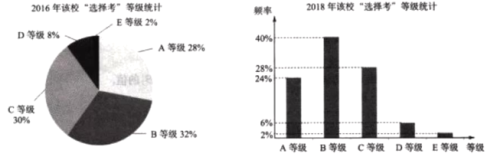
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com