Question

已知f(x)是二次函数，不等式f(x)＜0的解集是(0,5)且f(x)在区间［-1,4］上的最大值是12.

(1)求f(x)的解析式；

(2)是否存在实数m,使得方程f(x)+=0在区间(m,m+1)内有且只有两个不等的实数根？若存在，求出m的取值范围；若不存在，说明理由.

Answer 1

思路分析：将二次函数的图象（抛物线）与相应的一元二次方程、一元二次不等式联系起来分析是问题(1)得以解决的法宝；从题设的二次函数的图象（抛物线）的几何特征，可知抛物线的对称轴为x=，且通过(-1,12)点，进而求出该函数的表示式；是否存在唯一的自然数m=3，使得方程h（x）=2x³-10x²+37=0在区间（m，m+1）内有且只有两个不同的实数根.

解：（1）f（x）=-x²+8x=-（x-4）²+16.

当t+1＜4即t＜3时，f（x）在［t，t+1］上单调递增，

h（t）=f（t+1）=-（t+1）²+8（t+1）=-t²+6t+7；

当t≤4≤t+1，即3≤t≤4时，h（t）=f（4）=16；

当t＞4时，f（x）在［t，t+1］上单调递减，h（t）=f（t）=-t²+8t.

综上，h（t）=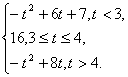

（2）函数y=f（x）的图象与y=g（x）的图象有且只有三个不同的交点，即函数

φ(x)=g(x)-f(x)的图象与x轴的正半轴有且只有三个不同的交点.

Qφ(x)=x²-8x+6lnx+m,

∴φ′(x)=2x-8+（x＞0）.

当x∈（0，1）时，φ′(x)＞0,φ(x)是增函数；

当x∈(0,3)时，φ′(x)＜0,φ(x)是减函数；

当x∈(3,+∞)时，φ′(x)＞0,φ(x)是增函数；

当x=1或x=3时，φ′(x)=0.

φ(x)_最大值=φ(1)=m-7，φ(x)_最小值=φ(3)=m+6ln3-15.

Q当x充分接近0时，φ(x)＜0，当x充分大时，φ(x)＞0

要使φ(x)的图象与x轴正半轴有三个不同的交点，必须且只须

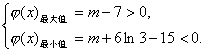
即7＜m＜15-6ln3.

所以存在实数m，使得函数y=f(x)与y=g(x)的图象有且只有三个不同的交点，m的取值范围为(7,15-6ln3).