
【题目】某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据![]() ,如下表所示:
,如下表所示:
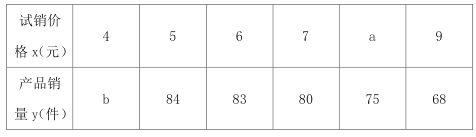
已知变量![]() 具有线性负相关关系,且
具有线性负相关关系,且![]() ,
, ![]() ,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲
,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出![]() 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,求这两个检测数据均为“理想数据”的概率.
科目:高中数学 来源: 题型:
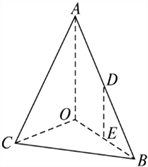
【题目】如图,在三棱锥![]() 中,
中, ![]() ⊥平面
⊥平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.(19)
的中点.(19)
(I)求![]() 到平面
到平面![]() 的距离;
的距离;
(II)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() ∥平面
∥平面![]() ,若存在,试确定
,若存在,试确定![]() 的位置,并证明此点满足要求;若不存在,请说明理由.
的位置,并证明此点满足要求;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N.
,以椭圆C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与椭圆C交于点M与点N. 
(1)求椭圆C的方程;
(2)求 ![]()
![]() 的最小值;
的最小值;
(3)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:|OR||OS|是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数a和b,定义运算“*”: ![]() ,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1,圆心角为 ![]() 的圆弧
的圆弧 ![]() 上有一点C.
上有一点C. 
(1)若C为圆弧AB的中点,点D在线段OA上运动,求| ![]() +
+ ![]() |的最小值;
|的最小值;
(2)若D,E分别为线段OA,OB的中点,当C在圆弧 ![]() 上运动时,求
上运动时,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察以下三个等式: sin215°﹣sin245°+sin15°cos45°=﹣ ![]() ,
,
sin220°﹣sin250°+sin20°cos50°=﹣ ![]() ,
,
sin230°﹣sin260°+sin30°cos60°=﹣ ![]() ;
;
猜想出一个反映一般规律的等式: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com