
分析 (1)将条件两边平方,化简可得$\overrightarrow{a}$•$\overrightarrow{b}$=0,可得直线l1与l2垂直;
(2)(1)的逆命题:若直线l1⊥l2,则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,也成立.由向量垂直的条件和完全平方公式,即可得到结论.
解答 解:(1)若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,
即为($\overrightarrow{a}$+$\overrightarrow{b}$)2=($\overrightarrow{a}$-$\overrightarrow{b}$)2,
即$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2+$\overrightarrow{b}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$,
即有$\overrightarrow{a}$•$\overrightarrow{b}$=0,
则$\overrightarrow{a}$⊥$\overrightarrow{b}$,
即有直线l1与l2垂直;
(2)(1)的逆命题:若直线l1⊥l2,
则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,也成立.
由直线l1⊥l2,可得$\overrightarrow{a}$⊥$\overrightarrow{b}$,
即$\overrightarrow{a}$•$\overrightarrow{b}$=0,即有$\overrightarrow{a}$2+$\overrightarrow{b}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$2+$\overrightarrow{b}$2-2$\overrightarrow{a}$•$\overrightarrow{b}$,
则($\overrightarrow{a}$+$\overrightarrow{b}$)2=($\overrightarrow{a}$-$\overrightarrow{b}$)2,
即有|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|.
点评 本题考查向量的数量积的性质,考查向量垂直的条件:数量积为0,向量的平方即为模的平方.考查推理能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 用方程表述 | 用函数零点表述 | |
| 若函数y=f(x)和y=g(x)的图象在(a,b)内有交点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [5,55] | B. | [5,50] | C. | [10,50] | D. | [10,55] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
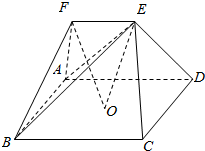 如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.
如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,△ABF是等边三角形,棱EF∥BC,且EF=$\frac{1}{2}$BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com