Question

【题目】某单位利用周末时间组织职工进行一次“健康之路、携手共筑”徒步走健身活动，有人参加，现将所有参加人员按年龄情况分为，六组，其频率分布直方图如图所示，已知岁年龄段中的参加者有人.

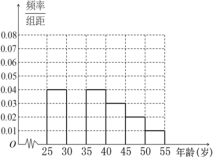
（1）求的值并补全频率分布直方图；

（2）从岁年龄段中采用分层抽样的方法抽取人作为活动的组织者，其中选取人作为领队，记选取的名领队中年龄在岁的人数为，求的分布列.

Answer 1

【答案】（1）40；见解析（2）见解析

【解析】

(1)根据岁年龄段中的参加者有人，再结合频率计算总人数，再根据频率之和为1求解第二组的频率，算出矩形的高补全即可.

(2)根据分层抽样的性质可得岁中有人，岁中有人，再根据超几何分布的方法列出分布列即可.

解：（1）年龄在之间的频率为，∵，∴.

∵第二组的频率为：

，

∴矩形高为.所以频率分布直方图如图所示.

（2）由（1）知，之间的人数为，又之间的人数为，

因为岁年龄段人数与岁年龄段人数的比值为，所以采用分层抽样抽取人，其中岁中有人，岁中有人.

由题意，随机变量的所有可能取值为.

，，.

所以随机变量的分布列为：

	1	2	3