练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题正确的是（ ）

    A.经过任意三点有且只有一个平面.

    B.过点有且仅有一条直线与异面直线垂直.

    C.一条直线与一个平面平行，它就和这个平面内的任意一条直线平行.

    D.面与平面相交，则公共点个数为有限个.

    【答案】B

    【解析】

    根据公理、异面直线垂直、线面平行、面面相交的知识对选项进行分析，由此确定正确选项.

    对于A选项，如果这三个点共线，经过这三个点不止一个平面，所以A选项错误.

    对于B选项，过上一点作，直线与确定平面，过作直线，则，则，而，所以，由于过平面外一点只能作平面一条垂线，所以B选项正确.

    对于C选项，一条直线与一个平面平行，它就和这个平面内的直线平行或异面，所以C选项错误.

    对于D选项，面与平面相交，则公共点个数为无限个，都在交线上，故D选项错误.

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某体育公司对最近6个月内的市场占有率进行了统计，结果如表：

    （1）可用线性回归模型拟合与之间的关系吗？如果能，请求出关于的线性回归方程，如果不能，请说明理由；

    （2）公司决定再采购，两款车扩大市场，，两款车各100辆的资料如表：

    平均每辆车每年可为公司带来收入500元，不考虑采购成本之外的其他成本，假设每辆车的使用寿命都是整数年，用每辆车使用寿命的频率作为概率，以每辆车产生利润的期望值作为决策依据，应选择采购哪款车型？

    参考数据：，，，．

    参考公式：相关系数；

    回归直线方程，其中，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，在一个周期内的图象如下图所示.

    （1）求函数的解析式；

    （2）设，且方程有两个不同的实数根，求实数m的取值范围和这两个根的和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列满足：，．

    （1）求数列的通项公式；

    （2）是否存在正整数，使得？若存在，求的最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

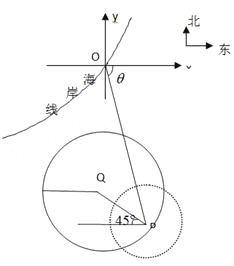
    【题目】在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O（如图）的东偏南方向300km的海面P处，并以20km/h的速度向西偏北方向移动，台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大，问几小时后该城市开始受到台风的侵袭？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，是半圆的直径，，为圆周上一点，平面，，，，.

    （1）求证：平面平面；

    （2）在线段上是否存在点，且使得平面？若存在，求出点的位置；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面，底面为正方形，，，分别是，的中点.

    （1）在平面内求一点，使平面，并证明你的结论；

    （2）求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正项等比数列满足，若存在两项，使得，则的最小值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某媒体为调查喜爱娱乐节目A是否与观众性别有关，随机抽取了30名男性和30名女性观众，抽查结果用等高条形图表示如图：

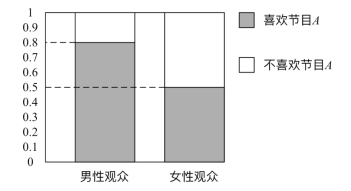
    根据该等高条形图，完成下列2×2列联表，并用独立性检验的方法分析，能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关？

    喜欢节目A

    不喜欢节目A

    总计

    男性观众

    女性观众

    总计

    60

    附：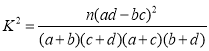

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    查看答案和解析>>

    同步练习册答案