
如图所示,已知线段|AB|=4,动圆O’与线段AB切于点C,且|AC|―|BC|=![]() ,过点A、B分别作⊙O’的切线,两切线相交于点P;且P、O’在AB的同侧.
,过点A、B分别作⊙O’的切线,两切线相交于点P;且P、O’在AB的同侧.
(1)建立适当的坐标系,当O’位置变化时,求动点P的轨迹E的方程;
(2)过点B作直线![]() 交曲线E于M、N,求△AMN面积的最小值.
交曲线E于M、N,求△AMN面积的最小值.

解:(1)以AB所在直线为![]() 轴,线段AB的垂直平分线为y轴,建立如图所示的直角坐标系,设点P为(
轴,线段AB的垂直平分线为y轴,建立如图所示的直角坐标系,设点P为(![]() ,y),
,y),
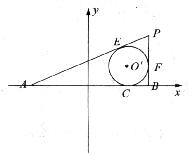
PA、PB分别切⊙![]() ,于E、F,则|PE|=|PF|,|AE|=|AC|,|BC|=|BF|,
,于E、F,则|PE|=|PF|,|AE|=|AC|,|BC|=|BF|,
又|AC|―|BC|=|PA|一|BP|=2![]() >0,
>0,
故点P的轨迹E是以A、B为焦点,实轴长为2![]() 的双曲线右支(除去与
的双曲线右支(除去与![]() 轴交点),
轴交点),
由题意知![]() =2
=2![]() ,c=2,则b2=2.故P点轨迹E的方程为
,c=2,则b2=2.故P点轨迹E的方程为![]() )
)
(2)设直线![]() 的方程为
的方程为![]()
联立方程组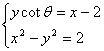
![]()
设M(![]() )、N(
)、N(![]() ),则yl+y2=
),则yl+y2=![]() , yly2=
, yly2=![]() ,
,
| yl-y2|2=( yl+y2)2-4 yly2=![]() ,
,
∴S△AMN=![]() =
=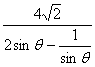
又![]() ,则
,则![]() ,而函数
,而函数![]() 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
故当sin![]() =1,即
=1,即![]() =
=![]() 时,A△AMN取得最小值,最小值为
时,A△AMN取得最小值,最小值为![]() .
.


科目:高中数学 来源: 题型:
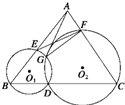 如图所示,已知D为△ABC的BC边上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过点C,D,交
如图所示,已知D为△ABC的BC边上一点,⊙O1经过点B,D,交AB于另一点E,⊙O2经过点C,D,交查看答案和解析>>
科目:高中数学 来源: 题型:
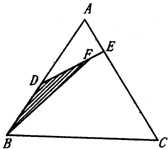 如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设
如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
| FG |
| FH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com