
���� ��1���������֪n��$\overline{x}$=3��$\overline{y}$=2��������ɵ�b��aֵ���ɵ÷��̣��ɻع鷽��x��ϵ��b���������У�
��2����x=2.5����ع鷽�����亯��ֵ���ɣ�
��� �⣺��1��������֪n=10��$\overline{x}$=3��$\overline{y}$=2��$\sum_{i=1}^{10}$xiyi=54��$\sum_{i=1}^{10}$xi2=170
��b�T$\frac{54-10��3��2}{170-10��{3}^{2}}$=-$\frac{3}{40}$��a=2-��-$\frac{3}{40}$����3=$\frac{89}{40}$��
������ع鷽��Ϊy=-$\frac{3}{40}$x+$\frac{89}{40}$������6�֣�
���ڱ���y��ֵ��x��ֵ���Ӷ���С����x��y֮���Ǹ���أ�����9�֣�
��2����x=2.5����ع鷽�̿���Ԥ��ü�ͥ���´���Ϊy=2.5-��-$\frac{3}{40}$��2.5+$\frac{89}{40}$��=0.4625��ǧԪ��������12�֣�
���� ���⿼�����Իع鷽�̵���⼰Ӧ�ã��������⣮


 ���Ӣ��������ϵ�д�
���Ӣ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=$\frac{k��}{2}$+$\frac{��}{8}$��k��Z | B�� | x=k��+$\frac{��}{8}$��k��Z | C�� | x=$\frac{k��}{2}$+$\frac{3��}{8}$��k��Z | D�� | x=k��+$\frac{3��}{8}$��k��Z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{256}$ | B�� | $\frac{1}{512}$ | C�� | $\frac{1}{1024}$ | D�� | $\frac{1}{2048}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$ | B�� | 2 | C�� | $\frac{1}{2}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | -4 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŸ߶������¿�һ��ѧ���Ծ��������棩 ���ͣ�ѡ����
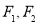 �ֱ�Ϊ˫����
�ֱ�Ϊ˫����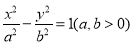 �����ҽ��㣬��
�����ҽ��㣬��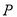 ��˫�����ϣ�����
��˫�����ϣ�����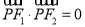 ����
����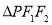 ������Բ�뾶�����Բ�뾶֮��Ϊ
������Բ�뾶�����Բ�뾶֮��Ϊ �����˫���ߵ�������Ϊ�� ��
�����˫���ߵ�������Ϊ�� ��
A��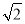 B��
B��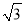 C��
C��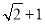 D��
D��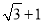
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com