
【题目】已知函数![]() ,函数图象在
,函数图象在![]() 处的切线与x轴平行.
处的切线与x轴平行.
(1)讨论方程![]() 根的个数;
根的个数;
(2)设![]() ,若对于任意的
,若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)先根据函数图象在![]() 处的切线与x轴平行可求
处的切线与x轴平行可求![]() 的值,然后求出函数的极值,从而可得根的个数;
的值,然后求出函数的极值,从而可得根的个数;
(2) 对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,可以转化为
成立,可以转化为![]() ,进而分别求解最值即可.
,进而分别求解最值即可.
解:(1)![]() ,
,
由题意知,![]() ,即
,即![]() ,解得
,解得![]() ,
,
故![]() ,此时
,此时![]() ,
,
则有:
x |
|
|
|
|
|
| + | 0 | - | td style="width:73.95pt; border-style:solid; border-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">+ | |
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以,当![]() 时,方程无根,当
时,方程无根,当![]() 或
或![]() 时,方程有一根,
时,方程有一根,
当![]() 或
或![]() 时,方程有两个根,当
时,方程有两个根,当![]() 时,方程有三个根;
时,方程有三个根;
(2)由题意可知,只需![]() ,
,
由(1)知,当![]() 时,
时,![]() ,
,
而![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
所以![]() ,因为
,因为![]() ,无解,
,无解,
![]() ,
,![]() ,无解,
,无解,
![]() ,
,![]() ,
,![]() 在
在![]() 单调递增,
单调递增,![]() ,
,
此时,![]() ,
,
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】将余弦函数的图象向右平移![]() 个单位后,再保持图象上点的纵坐标不变,横坐标变为原来的一半,得到函数
个单位后,再保持图象上点的纵坐标不变,横坐标变为原来的一半,得到函数![]() 的图象,下列关于
的图象,下列关于![]() 的叙述正确的是( )
的叙述正确的是( )
A. 最大值为![]() ,且关于
,且关于![]() 对称
对称
B. 周期为![]() ,关于直线
,关于直线![]() 对称
对称
C. 在![]() 上单调递增,且为奇函数
上单调递增,且为奇函数
D. 在![]() 上单调递减,且为偶函数
上单调递减,且为偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 为实数)有极值,且在
为实数)有极值,且在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(1)求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设函数![]() 试证明:
试证明:![]() 在
在![]() 上恒成立并证明
上恒成立并证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造![]() 、
、![]() 型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张
型两类桌子,每张桌子需木工和漆工梁道工序完成.已知木工做一张![]() 、
、![]() 型型桌子分别需要1小时和2小时,漆工油漆一张
型型桌子分别需要1小时和2小时,漆工油漆一张![]() 、
、![]() 型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张
型型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张![]() 、
、![]() 型型桌子分别获利润2千元和3千元.
型型桌子分别获利润2千元和3千元.
(1)列出满足生产条件的数学关系式,并画出可行域;
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
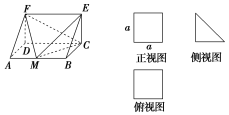
【题目】一个多面体的直观图和三视图如图所示,点M是AB上的动点,记四面体EFMC的体积为V1,多面体ADF-BCE的体积为V2,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.不是定值,随点M位置的变化而变化
D.不是定值,随点M位置的变化而变化
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地图上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高位10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.

(1)若圆形标志物半径为25m,以PG所在直线为X轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即![]() )的正切值为
)的正切值为![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com