
【题目】若函数h(x)满足
①h(0)=1,h(1)=0;
②对任意a∈[0,1],有h(h(a))=a;
③在(0,1)上单调递减.则称h(x)为补函数.已知函数h(x)= ![]() (λ>﹣1,p>0)
(λ>﹣1,p>0)
(1)判函数h(x)是否为补函数,并证明你的结论;
(2)若存在m∈[0,1],使得h(m)=m,若m是函数h(x)的中介元,记p= ![]() (n∈N+)时h(x)的中介元为xn , 且Sn=
(n∈N+)时h(x)的中介元为xn , 且Sn= ![]() ,若对任意的n∈N+ , 都有Sn<
,若对任意的n∈N+ , 都有Sn< ![]() ,求λ的取值范围;
,求λ的取值范围;
(3)当λ=0,x∈(0,1)时,函数y=h(x)的图象总在直线y=1﹣x的上方,求P的取值范围.
【答案】
(1)
解:函数h(x)是补函数,证明如下:
①h(0)= ![]() =1,h(1)=
=1,h(1)= ![]() =0;
=0;
②任意a∈[0,1],有h(h(a))=h( ![]() )=
)=  =a
=a
③令g(x)=(h(x))p,有g′(x)= ![]() =
= ![]() ,
,
又因为λ>﹣1,p>0,
所以当x∈(0,1)时,g′(x)<0,所以g(x)在(0,1)上是减函数,故h(x)在(0,1)上是减函数
由上证,函数h(x)是补函数
(2)
解:当p= ![]() (n∈N*),由h(x)=x得
(n∈N*),由h(x)=x得 ![]() ,
,
(i)当λ=0时,中介元xn= ![]() ,
,
(ii)当λ>﹣1且λ≠0时,由(*)得 ![]() =
= ![]() ∈(0,1)或
∈(0,1)或 ![]() =
= ![]() (0,1),得中介元xn=
(0,1),得中介元xn= ![]() ,
,
综合(i)(ii):对任意的λ>﹣1,中介元为xn= ![]() ,
,
于是当λ>﹣1时,有Sn= ![]() =
= ![]() =
= ![]() ,
,
当n无限增大时, ![]() 无限接近于0,Sn无限接近于
无限接近于0,Sn无限接近于 ![]() ,
,
故对任意的非零自然数n,Sn< ![]() 等价于
等价于 ![]() ,即λ∈[3,+∞)
,即λ∈[3,+∞)
(3)
解:当λ=0时,h(x)= ![]() ,中介元为
,中介元为  .
.
 ≤
≤ (ii)当p>1时,依题意只需 ![]() >1﹣x在x∈(0,1)时恒成立,也即xp+(1﹣x)p<1在x∈(0,1)时恒成立
>1﹣x在x∈(0,1)时恒成立,也即xp+(1﹣x)p<1在x∈(0,1)时恒成立
设φ(x)=xp+(1﹣x)p,x∈(0,1),则φ′(x)=p(xp﹣1﹣(1﹣x)p﹣1)
令φ′(x)=0,得x= ![]() ,且当x∈(0,
,且当x∈(0, ![]() )时,φ′(x)<0,当x∈(
)时,φ′(x)<0,当x∈( ![]() ,1)时,φ′(x)>0,又φ(0)=φ(1)=1,所以x∈(0,1)时,φ(x)<1恒成立.
,1)时,φ′(x)>0,又φ(0)=φ(1)=1,所以x∈(0,1)时,φ(x)<1恒成立.
综上,p的取值范围是(1,+∞)
【解析】(1)可通过对函数h(x)= ![]() (λ>﹣1,p>0)进行研究,探究其是否满足补函数的三个条件来确定函数是否是补函数;
(λ>﹣1,p>0)进行研究,探究其是否满足补函数的三个条件来确定函数是否是补函数;
(2)由题意,先根据中介元的定义得出中介元xn通式,代入Sn= ![]() ,计算出和,然后结合极限的思想,利用Sn<
,计算出和,然后结合极限的思想,利用Sn< ![]() 得到参数的不等式,解出它的取值范围;
得到参数的不等式,解出它的取值范围;
(3)λ=0,x∈(0,1)时,对参数p分类讨论由函数y=h(x)的图象总在直线y=1﹣x的上方这一位置关系进行转化,解出p的取值范围.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】乒乓球比赛规则规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换.每次发球,胜方得1分,负方得0分.设在甲、乙的比赛中,每次发球,发球方得1分的概率为0.6,各次发球的胜负结果相互独立.甲、乙的一局比赛中,甲先发球.
(1)求开始第4次发球时,甲、乙的比分为1比2的概率;
(2)ξ表示开始第4次发球时乙的得分,求ξ的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,新街口某新开业的商场在过去一个月内(以30天计),顾客人数![]() (千人)与时间
(千人)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]() (
(![]() ),人均消费
),人均消费![]() (元)与时间
(元)与时间![]() (天)的函数关系近似满足
(天)的函数关系近似满足![]()
(1)求该商场的日收益![]() (千元)与时间
(千元)与时间![]() (天)(
(天)(![]() ,
, ![]() )的函数关系式;
)的函数关系式;
(2)求该商场日收益的最小值(千元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分,众数,中位数;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在[50,90)之外的人数.
)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| 1:1 | 2:1 | 3:4 | 4:5 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在极坐标系和直角坐标系中,极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,直线
轴的正半轴重合,直线![]() :
:![]() (
(![]() 为参数),圆
为参数),圆![]() :
:![]() .
.
(Ⅰ)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)已知![]() 是直线
是直线![]() 上一点,
上一点,![]() 是圆
是圆![]() 上一点,求
上一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),设![]() ,
,
(1)若f(-1)=0,且对任意实数x均有f(x)≥0成立,求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0,且f(x)满足f(-x)=f(x),试比较F(m)+F(n)的值与0的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,∠ACB=45°,BC=3,过动点A作AD⊥BC,垂足D在线段BC上且异于点B,连接AB,沿AD将△ABD折起,使∠BDC=90°(如图2所示), 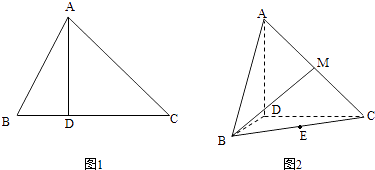
(1)当BD的长为多少时,三棱锥A﹣BCD的体积最大;
(2)当三棱锥A﹣BCD的体积最大时,设点E,M分别为棱BC,AC的中点,试在棱CD上确定一点N,使得EN⊥BM,并求EN与平面BMN所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com