
【题目】设a为实数,函数f(x)=![]() +a
+a![]() +a
+a![]() .
.
(1)设t=![]() ,求t的取值范图;
,求t的取值范图;
(2)把f(x)表示为t的函数h(t);
(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.
【答案】(1)[![]() ,2]; (2)h(t)=at+
,2]; (2)h(t)=at+![]() ,
,![]() ≤t≤2; (3)g(a)=
≤t≤2; (3)g(a)=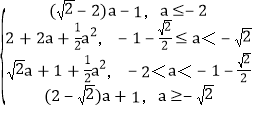 ..
..
【解析】
(1)将t=![]() 两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得
两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得![]() =
=![]() ,可得h(t)的解析式;(3)求得h(t)=
,可得h(t)的解析式;(3)求得h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,对称轴为t=-a,讨论对称轴与区间[
a2,对称轴为t=-a,讨论对称轴与区间[![]() ,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
(1)t=![]() ,可得t2=2+2
,可得t2=2+2![]() ,
,
由0≤1-x2≤1,可得2≤t2≤4,
又t≥0可得![]() ≤t≤2,
≤t≤2,
即t的取值范围是[![]() ,2];
,2];
(2)由(1)可得![]() =
=![]() ,
,
即有h(t)=at+![]() ,
,![]() ≤t≤2;
≤t≤2;
(3)由h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,
a2,
对称轴为t=-a,
当-a≥2即a≤-2时,h(t)在[![]() ,2]递减,
,2]递减,
可得最大值M(a)=h(![]() )=
)=![]() a;最小值m(a)=h(2)=1+2a,
a;最小值m(a)=h(2)=1+2a,
则g(a)=(![]() -2)a-1;
-2)a-1;
当-a≤![]() 即a≥-
即a≥-![]() 时,h(t)在[
时,h(t)在[![]() ,2]递增,
,2]递增,
可得最大值M(a)=h(2)=1+2a;最小值m(a)=h(![]() )=
)=![]() a,
a,
则g(a)=(2-![]() )a+1;
)a+1;
当![]() <-a<2即-2<a<-
<-a<2即-2<a<-![]() 时,h(t)的最小值为m(a)=h(-a)=-1-
时,h(t)的最小值为m(a)=h(-a)=-1-![]() a2,
a2,
若-1-![]() ≤a<-
≤a<-![]() ,则h(2)≥h(
,则h(2)≥h(![]() ),可得h(t)的最大值为M(a)=h(2)=1+2a,
),可得h(t)的最大值为M(a)=h(2)=1+2a,
可得g(a)=2+2a+![]() a2;
a2;
若-2<a<-1-![]() ,则h(2)<h(
,则h(2)<h(![]() ),可得h(t)的最大值为M(a)=h(
),可得h(t)的最大值为M(a)=h(![]() )=
)=![]() a,
a,
可得g(a)=![]() a+1+
a+1+![]() a2;
a2;
综上可得g(a)=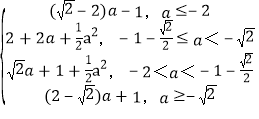 .
.


科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若p=2且∠BFD=90°时,求圆F的方程;
(2)若A,B,F三点在同一直线m上,设直线m与抛物线C的另一个交点为E,在y轴上求一点G,使得∠OGE=∠OGA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2 , 这两条曲线在第一象限的交点为P,△PF1F2 是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2 , 则e1e2 的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的值域为[0,+∞),求实数a的取值范围;
的值域为[0,+∞),求实数a的取值范围;
(2)若关于x的不等式F(x)>af(x)+12恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资![]() 类产品的收益与投资额成正比,投资
类产品的收益与投资额成正比,投资![]() 类产品的收益与投资额的算术平方根成正比.已知投资1万元时
类产品的收益与投资额的算术平方根成正比.已知投资1万元时![]() 两类产品的收益分别为0.125万元和0.5万元.
两类产品的收益分别为0.125万元和0.5万元.
(1)分别写出![]() 两类产品的收益与投资额的函数关系;
两类产品的收益与投资额的函数关系;
(2)该家庭有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com