
【题目】设函数f(x)=x2eax , a>0.
(1)证明:函数y=f(x)在(0,+∞)上为增函数;
(2)若方程f(x)﹣1=0有且只有两个不同的实数根,求实数a的值.
【答案】
(1)证明:f(x)的定义域R,求导,f′(x)=2xeax+ax2eax=xeax(ax+2),
当x∈(0,+∞)时,a>0,则eax>0,则xeax(ax+2)>0,
则f′(x)>0,
∴函数y=f(x)在(0,+∞)上为增函数
(2)令f′(x)=0,记得x=﹣v或x=0,
x | (﹣∞,﹣ |
| ( | 0 | (0,+∞) |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
则当x=﹣ ![]() 时,函数有极大值f(﹣
时,函数有极大值f(﹣ ![]() )=
)= ![]() ,
,
当x=0时,函数有极小值f(0)=0,
当x<0时,f(x)>0,x→﹣∞时,f(x)→0,x→+∞时,f(x)→+∞,
由f(x)﹣1=0,即f(x)=1有且只有两个不同的实数根,
即 ![]() =1,解得:a=
=1,解得:a= ![]() ,(负根舍去)
,(负根舍去)
实数a的值 ![]()
【解析】(1)求导,由x∈(0,+∞)则f′(x)>0,则函数y=f(x)在(0,+∞)上为增函数;(2)求导,f′(x)=0,根据函数的单调性即可求得f(x)极大值,由f(x)=1有且只有两个不同的实数根,即 ![]() =1,即可求得实数a的值.
=1,即可求得实数a的值.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】一个盒子中装有4个编号依次为1、2、3、4的球,这4个球除号码外完全相同,先从盒子中随机取一个球,该球的编号为X,将球放回袋中,然后再从袋中随机取一个球,该球的编号为Y
(1)列出所有可能结果.
(2)求事件A=“取出球的号码之和小于4”的概率.
(3)求事件B=“编号X<Y”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)猜想Sn的表达式,并用数学归纳法证明;
(2)设bn= ![]() ,n∈N* , 求bn的最大值.
,n∈N* , 求bn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某人的射击技术情况,在他的训练记录中抽取50次检验,他的命中环数如下:10,5,5,8,7,8,6,9,7,8,6,6,5,6,7,8,10,9,7,9,8,7,6,5,9,9,8,8,5,8,6,7,6,9,6,8,8,8,6,7,6,8,107,10,8,7,7,9,5
(1)列出频率分布表
(2)画出频率分布的直方图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接党的“十九”大的召开,某校组织了“歌颂祖国,紧跟党走”党史知识竞赛,从参加考试的学生中抽出50名学生,将其成绩(满分100分,成绩均为整数)分成六段![]() ,
, ![]() ,…,
,…, ![]() 后绘制频率分布直方图(如下图所示)
后绘制频率分布直方图(如下图所示)
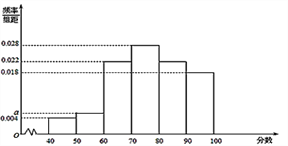
(Ⅰ)求频率分布图中![]() 的值;
的值;
(Ⅱ)估计参加考试的学生得分不低于80的概率;
(Ⅲ)从这50名学生中,随机抽取得分在![]() 的学生2人,求此2人得分都在
的学生2人,求此2人得分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com