
【题目】已知z为复数,ω=z+ ![]() 为实数,
为实数,
(1)当﹣2<ω<10,求点Z的轨迹方程;
(2)当﹣4<ω<2时,若u= ![]() (α>0)为纯虚数,求:α的值和|u|的取值范围.
(α>0)为纯虚数,求:α的值和|u|的取值范围.
【答案】
(1)解:设z=x+yi,x,y∈R,
则ω=z+ ![]() =x+yi+
=x+yi+ ![]() =x+yi+
=x+yi+ ![]() =
= ![]() +
+ ![]() i为实数,
i为实数,
∴y﹣ ![]() =0,∴y=0,或x2+y2=9.
=0,∴y=0,或x2+y2=9.
①y=0时,ω=x+ ![]()
∵﹣2<ω<10,∴﹣2< ![]() <10,
<10,
x>0时,解得1<x<9.x<0时,x∈.
综上可得:y=0时,点Z的轨迹方程是 ![]() .
.
②x2+y2=9时.
ω=2x,
∵﹣2<ω<10,∴﹣2<2x<10,
解得﹣1<x<5.
因此x2+y2=9时.可得:点Z的轨迹方程是x2+y2=9(﹣1<x<5)
(2)解:由(1)可得:①y=0时,ω=x+ ![]()
∵﹣4<ω<2,∴﹣4< ![]() <2,
<2,
∵x<0时, ![]() ≤﹣6;x>0时,
≤﹣6;x>0时, ![]() ≥6.
≥6.
综上可得:y=0时,x∈,点Z的轨迹无方程.
②x2+y2=9时.
ω=2x,
∵﹣4<ω<2,∴﹣4<2x<2,
解得﹣2<x<1.
∵u= ![]() (α>0)为纯虚数,
(α>0)为纯虚数,
u= ![]() =
= ![]() ,
,
∴α2﹣9=0,2yα≠0,
解得α=3,y≠0.
∴u= ![]() =
= ![]() ,
,
∵x∈(﹣2,1),
∴|u|= ![]() =
= ![]() =
= ![]() ∈
∈ ![]() .
.
∴α=3,|u|∈ ![]() /p>
/p>
【解析】(1)设z=x+yi,x,y∈R,则ω= ![]() +
+ ![]() i为实数,可得y﹣
i为实数,可得y﹣ ![]() =0,因此y=0,或x2+y2=9.通过分类讨论即可得出.(2)由(1)可得:①y=0时,ω=x+
=0,因此y=0,或x2+y2=9.通过分类讨论即可得出.(2)由(1)可得:①y=0时,ω=x+ ![]() ,由﹣4<ω<2,可得﹣4<
,由﹣4<ω<2,可得﹣4< ![]() <2,利用基本不等式的性质即可得出.②x2+y2=9时.ω=2x,由于﹣4<ω<2,即可得出x的取值范围.由u=
<2,利用基本不等式的性质即可得出.②x2+y2=9时.ω=2x,由于﹣4<ω<2,即可得出x的取值范围.由u= ![]() (α>0)为纯虚数,化简可得α,再利用模的计算公式、函数的单调性即可得出.
(α>0)为纯虚数,化简可得α,再利用模的计算公式、函数的单调性即可得出.
【考点精析】解答此题的关键在于理解复数的乘法与除法的相关知识,掌握设![]() 则
则![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
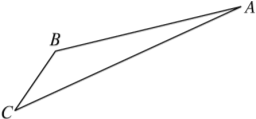
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣bx+3.
(1)若函数f(x)为R上的偶函数,求b的值.
(2)若函数f(x)在(﹣∞,2]上单调递减,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取3个点,记落在直线![]() 右下方的点的个数为
右下方的点的个数为![]() ,求
,求![]() 的分布列以及期望.
的分布列以及期望.
参考公式: 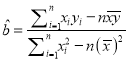 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱ABCD﹣A1B1C1D1 , DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为 ![]() 的等比数列,
的等比数列, 
(1)求异面直线AD1与BD所成角的大小;
(2)求二面角B﹣AD1﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定投掷飞镖3次为一轮,若3次中至少两次投中8环以上为优秀,现采用随机模拟实验的方法估计某人投掷飞镖的情况:先由计算器产生随机数0或1,用0表示该次投标未在8环以上,用1表示该次投标在8环以上;再以每三个随机数作为一组,代表一轮的结果,经随机模拟实验产生了如下20组随机数:
101 111 011 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,该选手投掷飞镖三轮,至少有一轮可以拿到优秀的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),当x∈(﹣∞,0)时,f(x)=﹣x2+mx﹣1.
(1)求f(x)的解析式;
(2)若方程f(x)=0有五个不相等的实数解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com