
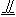
(1)求证:B1D1∥平面CMN;
(2)求点B1到平面CMN的距离.
解法一:(1)证明:∵M、N为B1C1和C1D1的中点,∴MN∥B1D1.?
∵MN![]() 平面CMN,∴B1D1∥面CMN.?
平面CMN,∴B1D1∥面CMN.?
(2)连结B1N、BM.?
设B1到CMN的距离为d.?
∵CC1⊥面B1MN,?
∴VB1—CMN?=VC—B1MN .?
∴S△CMN·d=S△B1MN·CC1.?
∵MN ![]()
![]() B1D1,?
B1D1,?
∴S△B1MN =![]() S△B1C1D1=
S△B1C1D1=![]() a2.?
a2.?
∵CC1⊥C1M,∴CM=![]() a.?
a.?
同理,CN=![]() a,MN=
a,MN=![]() a,连结CO1.?
a,连结CO1.?
∵O1为MN中点,∴CO1⊥MN.?
∴CO1=![]() a.?
a.?
∴S△CMN?=![]() CO1·MN=
CO1·MN=![]() a2.?
a2.?
∴![]() a2·a=
a2·a=![]() a2·d.∴d=
a2·d.∴d=![]() .?
.?
解法二:(1)证明:以D为原点,建立空间直角坐标系.?
∴D1(0,0,a),B1(a,a,a),C1(0,a,a).?
∵M为B1C1中点,∴M(![]() ,a,a).?
,a,a).?
同理,N(0,![]() ,a).?
,a).?
∴![]() =(-
=(-![]() ,-
,-![]() ,0),
,0),![]() =(a,a,0).?
=(a,a,0).?
∴![]() =-
=-![]() .
.
∴![]() 与
与![]() 共线.
共线.
∴B1D1∥面CMN.?
(2)作B1在面CMN上的射影E,设E(x,y,z).??
∴B1E⊥面MNC.?
∴![]() =(x-a,y-a,z-a).?
=(x-a,y-a,z-a).?
∴B1E⊥MN,B1E⊥CM.?
∵![]() =(-
=(-![]() ,-
,-![]() ,0),
,0),![]() =(
=(![]() ,0,a),?
,0,a),?
∵E在CO1上,∴![]() ∥
∥![]() .
.
∴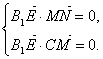 ?
?
∵O1(![]() a,
a,![]() a,a),?
a,a),?
∴![]() =(
=(![]() a,
a, ![]() a,a).?
a,a).?
∴y=![]() a.∴|
a.∴|![]() |=
|=![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
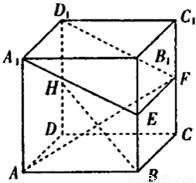
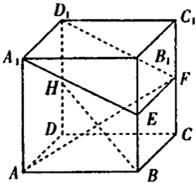 如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点.
如图所示,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、H分别是棱BB1、CC1、DD1的中点.查看答案和解析>>
科目:高中数学 来源:单元双测 同步达标活页试卷 高二数学(下A) 人教版 题型:047
| |||||||||||
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省汕尾市陆丰东海中学高二(上)期末数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省温州市十校联合体高三(上)期中数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com