
【题目】十九大提出,加快水污染防治,建设美丽中国![]() 根据环保部门对某河流的每年污水排放量
根据环保部门对某河流的每年污水排放量![]() 单位:吨
单位:吨![]() 的历史统计数据,得到如下频率分布表:
的历史统计数据,得到如下频率分布表:
污水量 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
将污水排放量落入各组的频率作为概率,并假设每年该河流的污水排放量相互独立.
(Ⅰ)求在未来3年里,至1年污水排放量![]() 的概率;
的概率;
(Ⅱ)该河流的污水排放对沿河的经济影响如下:当![]() 时,没有影响;当
时,没有影响;当![]() 时,经济损失为10万元;当
时,经济损失为10万元;当![]() 时,经济损失为60万元
时,经济损失为60万元![]() 为减少损失,现有三种应对方案:
为减少损失,现有三种应对方案:
方案一:防治350吨的污水排放,每年需要防治费![]() 万元;
万元;
方案二:防治310吨的污水排放,每年需要防治费2万元;
方案三:不采取措施.
试比较上述三种方案,哪种方案好,并请说明理由.
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某同学在研究函数f(x)=![]() (x∈R)时,分别给出下面几个结论:
(x∈R)时,分别给出下面几个结论:
①等式f(-x)=-f(x)在x∈R时恒成立;
②函数f(x)的值域为(-1,1);
③若x1≠x2,则一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三个根.
其中正确结论的序号有______.(请将你认为正确的结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是双曲线左、右两支上关于坐标原点
分别是双曲线左、右两支上关于坐标原点![]() 对称的两点,且直线
对称的两点,且直线![]() 的斜率为
的斜率为![]() .
.![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,若原点
的中点,若原点![]() 在以线段
在以线段![]() 为直径的圆上,则双曲线的离心率为( )
为直径的圆上,则双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家计了一个招标方案:两家公司从6个招标问题中随机抛取3个问题,已知这6个问中,甲公司可正确回答其中的4道题,而乙公司能正确回答每道题目的概率均为![]() ,且甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,且甲、乙两家公司对每题的回答都是相互独立,互不影响的.
(I)求甲、乙两家公司共答对2道题的概率;
(II)设X为乙公司正确回答的题数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知四边形BCDE为直角梯形,![]() ,
,![]() ,且
,且![]() ,A为BE的中点
,A为BE的中点![]() 将
将![]() 沿AD折到
沿AD折到![]() 位置
位置![]() 如图
如图![]() ,连结PC,PB构成一个四棱锥
,连结PC,PB构成一个四棱锥![]() .
.

![]() Ⅰ
Ⅰ![]() 求证
求证![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 平面ABCD.
平面ABCD.
![]() 求二面角
求二面角![]() 的大小;
的大小;
![]() 在棱PC上存在点M,满足
在棱PC上存在点M,满足![]() ,使得直线AM与平面PBC所成的角为
,使得直线AM与平面PBC所成的角为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
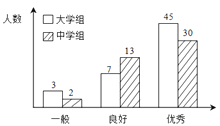
若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95﹪的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注: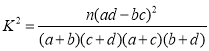 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为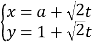 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com