
【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:解法1:设⊙M的方程为:x2+y2+Dx+Ey+F=0,
则由题意得 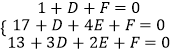 ,解得
,解得 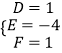 ,
,
∴⊙M的方程为x2+y2﹣2x﹣4y+1=0,或(x﹣1)2+(y﹣2)2=4
解法2:∵A(1,0),B(1,4)的横坐标相同,故可设M(m,2),
由MA2=MC2得(m﹣1)2+4=(m﹣3)2,解得m=1
∴⊙M的方程为(x﹣1)2+(y﹣2)2=4,或x2+y2﹣2x﹣4y+1=0
解法3:∵A(1,0),B(1,4),C(3,2),∴ ![]() ,
,
∴ ![]() ,则△ACB是等腰直角三角形,
,则△ACB是等腰直角三角形,
因而△ACB圆心为(1,2),半径为2,
∴⊙M的方程为(x﹣1)2+(y﹣2)2=4
(2)解:当直线l与x轴垂直时,l方程为x=0,它截⊙M得弦长恰为2 ![]()
当直线l的斜率存在时,设l:y=kx+4
∵圆心到直线y=kx+4的距离d= ![]()
由勾股定理得 ![]() ,解得
,解得 ![]()
故直线l的方程为x=0或3x+4y﹣16=0
【解析】(1)解法1:设⊙M的方程为一般式,根据条件列出方程组,求解后即可求出⊙M的方程;解法2:根据A(1,0),B(1,4)的横坐标相同设M(m,2),由半径相等和两点之间的距离公式列出方程求出m,可得⊙M的方程;解法3:由向量的坐标运算求出 ![]() ,由向量的数量积运算求出
,由向量的数量积运算求出 ![]() 和模,判断出△ACB是等腰直角三角形,由直角三角形外接圆的性质求出⊙M的方程;(2)对直线l的斜率存在问题分类讨论,根据点到直线的距离公式和弦长公式列出方程,求出直线的斜率,即可得到直线方程.
和模,判断出△ACB是等腰直角三角形,由直角三角形外接圆的性质求出⊙M的方程;(2)对直线l的斜率存在问题分类讨论,根据点到直线的距离公式和弦长公式列出方程,求出直线的斜率,即可得到直线方程.
【考点精析】根据题目的已知条件,利用圆的一般方程的相关知识可以得到问题的答案,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】为了参加第二届全国数学建模竞赛,长郡中学在高二年级举办了一次选拔赛,共有60名高二学生报名参加,按照不同班级统计参赛人数,如表所示:
班级 | 宏志班 | 珍珠班 | 英才班 | 精英班 |
参赛人数 | 20 | 15 | 15 | 10 |
(Ⅰ)从这60名高二学生中随机选出2人,求这2人在同一班级的概率;
(Ⅱ)现从这60名高二学生中随机选出2人作为代表,进行大赛前的发言,设选出的2人中宏志班的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,已知a=2,b=3,cosC= ![]() .
.
(1)求△ABC的面积;
(2)求sin(C﹣A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[ ![]() ],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+
],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+ ![]() ②f(x)=﹣x2+4x ③f(x)=sin
②f(x)=﹣x2+4x ③f(x)=sin ![]() x ④f(x)=
x ④f(x)= 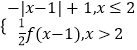 ,具有“反衬性”的为|( )
,具有“反衬性”的为|( )
A.②③
B.①③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|﹣|2x﹣a|,a∈R.
(1)当a=3时,解不等式f(x)>0;
(2)当x∈(﹣∞,2)时,f(x)<0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
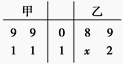
【题目】如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题(满分12分)的得分情况.乙组某个数据的个位数模糊,记为x,已知甲、乙两组的平均成绩相同.
(1)求x的值,并判断哪组学生成绩更稳定;
(2)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从正方体ABCD﹣A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
1)矩形的4个顶点;
2)每个面都是等边三角形的四面体的4个顶点;
3)每个面都是直角三角形的四面体的4个顶点;
4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确结论的个数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com