
【题目】多面体![]() 中,平面
中,平面![]() ∥平面
∥平面![]() ,
,![]() ∥
∥![]() ,
,![]() 平面
平面![]() ,
,![]() 为直角梯形,
为直角梯形,![]() ,
,![]() .
.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如下图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,已知点
,已知点![]() 和
和 都在椭圆上,其中
都在椭圆上,其中![]() 为椭圆的离心率.
为椭圆的离心率.

(1)求椭圆的方程;
(2)设![]() ,
, ![]() 是椭圆上位于
是椭圆上位于![]() 轴上方的两点,且直线
轴上方的两点,且直线![]() 与直线
与直线![]() 平行,
平行, ![]() 与
与![]() 交于点
交于点![]() ,
,
(i)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(ii)求证: ![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高一学生的视力健康状况,在高一年级体检活动中采用统一的标准对数视力表,按照《中国学生体质健康监测工作手册》的方法对1039名学生进行了视力检测,判断标准为:双眼裸眼视力![]() 为视力正常,
为视力正常, ![]() 为视力低下,其中
为视力低下,其中![]() 为轻度,
为轻度, ![]() 为中度,
为中度, ![]() 为重度.统计检测结果后得到如图所示的柱状图.
为重度.统计检测结果后得到如图所示的柱状图.
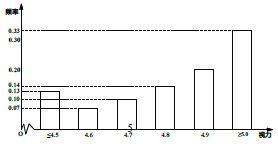
(1)求该校高一年级轻度近视患病率;
(2)根据保护视力的需要,需通知检查结果为“重度近视”学生的家长带孩子去医院眼科进一步检查和确诊,并开展相应的矫治,则该校高一年级需通知的家长人数约为多少人?
(3)若某班级6名学生中有2人为视力正常,则从这6名学生中任选2人,恰有1人视力正常的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别为双曲线
分别为双曲线![]() 的左右焦点,左右顶点为
的左右焦点,左右顶点为![]() 、
、![]() ,
,![]() 是双曲线上任意一点,则分别以线段
是双曲线上任意一点,则分别以线段![]() 、
、![]() 为直径的两圆的位置关系为( )
为直径的两圆的位置关系为( )
A. 相交B. 相切C. 相离D. 以上情况均有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() 函数
函数![]() ,其图象的两条相邻对称轴间的距离为
,其图象的两条相邻对称轴间的距离为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图象上各点的横坐标缩短为原来的
的图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,再将图象向右平移
,纵坐标不变,再将图象向右平移![]() 个单位,得到
个单位,得到![]() 的图象,求
的图象,求![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且ω>0,
,且ω>0,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知 ,且函数f(x)的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求f(θ)的值;
,求f(θ)的值;
(2)求函数f(x)在[0,2π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求续驶里程在![]() 的车辆数;
的车辆数;
(2)求续驶里程的平均数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com