
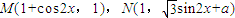 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且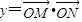 (O为坐标原点).
(O为坐标原点). 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;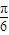 的范围进而利用正弦函数的性质求得函数的最大值,求得a.
的范围进而利用正弦函数的性质求得函数的最大值,求得a.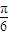 )+2,然后利用三角函数图象平移的法则求得答案.
)+2,然后利用三角函数图象平移的法则求得答案.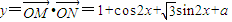 ,
,
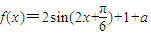 ,
,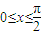 ,所以
,所以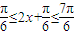 ,
,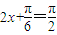 即
即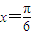 时f(x)取最大值3+a,
时f(x)取最大值3+a,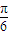 个单位得到函数
个单位得到函数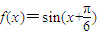 的图象;
的图象;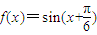 的图象保持纵坐标不变,横坐标缩短为原来的
的图象保持纵坐标不变,横坐标缩短为原来的 得到函数
得到函数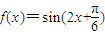 的图象;
的图象;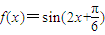 的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数
的图象保持横坐标不变,纵坐标伸长为原来的2倍得到函数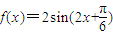 的图象;
的图象;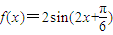 的图象向上平移2个单位,得到函数
的图象向上平移2个单位,得到函数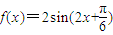 +2的图象
+2的图象

科目:高中数学 来源:2012-2013学年贵州省毕节地区黔西二中高二(上)期中数学试卷(解析版) 题型:解答题
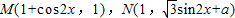 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且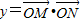 (O为坐标原点).
(O为坐标原点).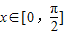 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;查看答案和解析>>
科目:高中数学 来源:2012年山东省普通高中学业水平考试数学样卷(四)(解析版) 题型:解答题
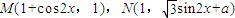 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点).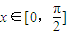 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市南丰中学高三(上)数学复习试卷C (必修4)(解析版) 题型:解答题
 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点). 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;查看答案和解析>>
科目:高中数学 来源:2011年高三数学一轮精品复习学案:2.1 函数及其表示(解析版) 题型:解答题
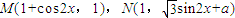 (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (O为坐标原点).
(O为坐标原点).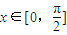 时,f(x)的最大值为4,求a的值;
时,f(x)的最大值为4,求a的值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com