
【题目】已知![]() ,
,![]() 是抛物线
是抛物线![]()
![]() 上的两点,若直线
上的两点,若直线![]() 过抛物线的焦点
过抛物线的焦点![]() 且倾斜角为
且倾斜角为![]() .
.![]() ,
,![]() 是
是![]() ,
,![]() 在准线上的射影.则下列命题正确的是( )
在准线上的射影.则下列命题正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 为锐角三角形.
为锐角三角形.
【答案】ABC
【解析】
对于选项A,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,再利用韦达定理,即可得到结论;
,再利用韦达定理,即可得到结论;
对于选项B,利用抛物线的定义和选项A中的结论,表示出![]() 即可;
即可;
对于选项C,由抛物线的定义,在直角三角形![]() 中,运用余弦函数的定义,即可得到
中,运用余弦函数的定义,即可得到![]() 的长,同理可得
的长,同理可得![]() 的长,即可判断;
的长,即可判断;
对于选项D,由![]() ,
,![]() 是
是![]() ,
,![]() 在准线上的射影,可求出
在准线上的射影,可求出![]() ,进而判断D错误.
,进而判断D错误.
解:对于选项A,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,
,
可得![]() ,所以
,所以![]() ,
,![]() ,选项A正确;
,选项A正确;
对于选项B,因为![]() 是过抛物线
是过抛物线![]() 的焦点的弦,
的焦点的弦,
所以由抛物线定义可得![]() ,
,
由选项A知,![]() ,
,![]() ,
,
所以![]() .
.
即![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]()
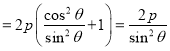 ,
,
当![]() 时,
时,![]() 也适合上式,所以
也适合上式,所以![]() ,选项B正确;
,选项B正确;
对于选项C,![]() ,
,
所以![]() ,同理可得
,同理可得![]() ,
,
所以![]() ,选项C正确;
,选项C正确;
对于选项D,由抛物线的定义可知,![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,则
,则![]() .
.
同理可得![]() .
.
因为![]() ,
,
所以![]() .
.
所以![]() 为直角三角形,选项D错误.
为直角三角形,选项D错误.
故选:ABC.


科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
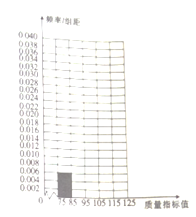
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”的证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,他需要通过四个科目的考试,其中科目二为场地考试.在一次报名中,每个学员有5次参加科目二考试的机会(这5次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试;若5次都没有通过,则需重新报名),其中前2次参加科目二考试免费,若前2次都没有通过,则以后每次参加科目二考试都需要交200元的补考费.某驾校对以往2000个学员第1次参加科目二考试进行了统计,得到下表:
考试情况 | 男学员 | 女学员 |
第1次考科目二人数 | 1200 | 800 |
第1次通过科目二人数 | 960 | 600 |
第1次未通过科目二人数 | 240 | 200 |
若以上表得到的男、女学员第1次通过科目二考试的频率分别作为此驾校男、女学员每次通过科目二考试的概率,且每人每次是否通过科目二考试相互独立.现有一对夫妻同时在此驾校报名参加了驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)若这对夫妻前2次参加科目二考试均没有通过,记这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元,求
元,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 上顶点为A,右焦点为F,直线
上顶点为A,右焦点为F,直线![]() 与圆
与圆![]() 相切,其中
相切,其中![]() .
.
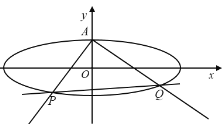
(1)求椭圆的方程;
(2)不过点A的动直线l与椭圆C相交于P,Q两点,且![]() ,证明:动直线l过定点,并且求出该定点坐标.
,证明:动直线l过定点,并且求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富市民的文化生活,市政府计划在一块半径为100m的扇形土地OAB上建造市民广场.规划设计如图:矩形EFGH(其中E,F在圆弧AB上,G,H在弦AB上)区域为运动休闲区,△OAB区域为文化展示区,其余空地为绿化区域,已知P为圆弧AB中点,OP交AB于M,cos∠POB=![]() ,记矩形EFGH区域的面积为Sm2.
,记矩形EFGH区域的面积为Sm2.
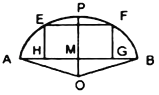
(1)设∠POF=θ(rad),将S表示成θ的函数;
(2)求矩形EFGH区域的面积S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂加工一批零件,加工过程中会产生次品,根据经验可知,其次品率![]() 与日产量
与日产量![]() (万件)之间满足函数关系式
(万件)之间满足函数关系式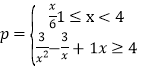 ,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
,已知每生产1万件合格品可获利2万元,但生产1万件次品将亏损1万元.(次品率=次品数/生产量).
(1)试写出加工这批零件的日盈利额![]() (万元)与日产量
(万元)与日产量![]() (万件)的函数;
(万件)的函数;
(2)当日产量为多少时,可获得最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com