Question

（08年长沙市模拟理）（13分）已知数列{a_n}的前n项和S_n满足S_n=-1，S_n+1+2S_n=-1（），数列{bn}的通项公式为。

（1）求数列的通项公式；

    （2）是否存在圆心在x轴上的圆C及互不相等的正整数n、m、k，使得三点A_n(b_n,a_n)，A_m(b_m,a_m),A_k(b_k,a_k)落在圆C上？说明理由。

Answer 1

解析：解析：（1），

两式相减得

又

，即数列是首项为-1，公比为-2的等比数列其通项公式是  4分

（2）不存在圆心在x轴上的圆C及互不相等的正整数n、m、k，使得三点A_n，A_m，A_k落在圆C上。  5分

假设存在圆心在x轴上的圆C及互不相等的正整数n、m、k，使得点三点A_n，A_m，A_k，即落在圆C上，不妨设n>m>k，设圆方程为：

x²+y²+Dx+F=0，从而9n²-24n+16+4^n-1+(3n-4)D+F=0①

9m²-24m+16+4^m-1+(3m+4)D+F=0，②

9k²-24k+16+4^k-1+（3k-4）D+F=0，③  7分

由①-②，②-③得：9(n+m)(n-m)-24(n-m)+(4^n-1-4^m-1)+3(n-m)D=0，

9(m+k)(m-k)-24(m-k)+(4^m-1-4^k-1)+3(m-k)D=0，

即④

，⑤

由④-⑤，得，

整理，得，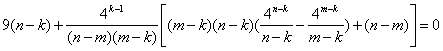

，

⑥   9分

设函数，

知函数是增函数

，与⑥式产生矛盾。

故不存在圆心在x轴上的圆C及互不相等的正整数n、m、k，使得三点An，A_m，A_k落在圆C上。